Aconteceu nos dias 11 e 12 de Novembro de 2016 a etapa nacional da Maratona de Programação em Belo Horizonte, MG, com realização da UFMG, CEFET-MG e PUC-Minas. O resultado completo pode ser conferido aqui. Em 2016, o Centro-Oeste teve como representantes as equipes “Where are the monkeys?” do INF-UFG, “Teorema de Offson” da UnB/FGA e “Turkeys” da UnB. As equipes terminaram em 9o, 14o e 16o respectivamente, sendo a equipe “Where are the monkeys?” premiada com uma medalha de bronze e reconhecida simbolicamente como a campeã do Centro-Oeste.
As 10 melhores equipes podem ser vistas na imagem abaixo.
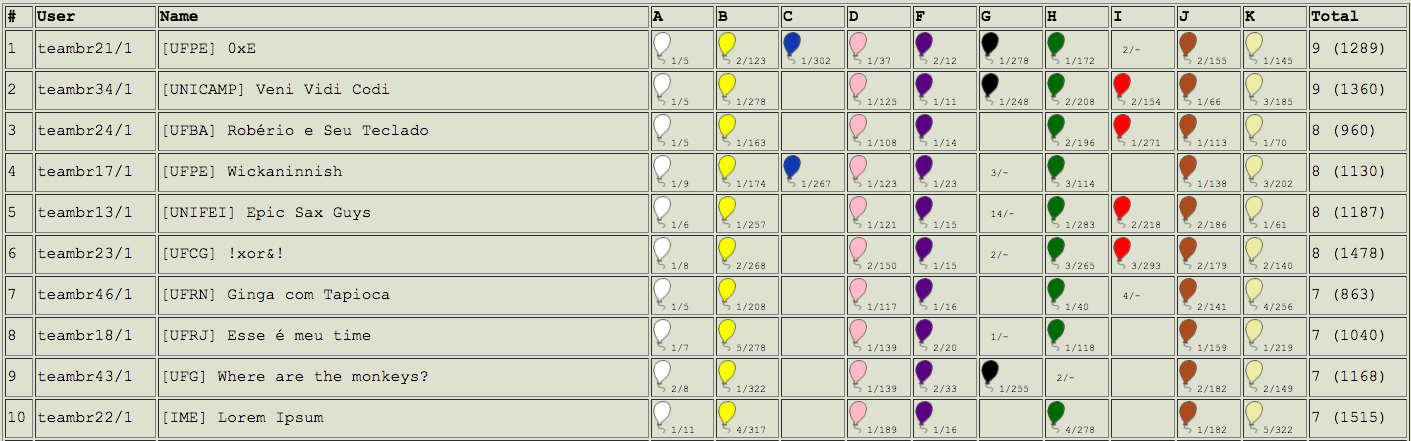
A prova esse ano estava bem balanceada e foi composta por 10 problemas bem interessantes. Dicas para solucionar os problemas e exemplos de implementação podem ser encontradas abaixo.
| Problema | Dificuldade | Técnica relacionada |
|---|---|---|
| A - Assigning Teams | balão++ | ad hoc |
| B - Back to the Future | fácil/médio | greedy, graphs |
| C - Counting Self-Rotating Subsets | médio/difícil | combinatorics, geometry |
| D - Dating On-Line | fácil | ad hoc, geometry |
| F - Farm robot | balão++ | ad hoc, implementation |
| G - Game of Matchings | médio/difícil | KMP, string matching |
| H - Hotel Rewards | médio | greedy |
| I - Internet Trouble | difícil | dynamic programming |
| J - Just in Time | fácil | graphs, math |
| K - Kill the Werewolf | médio | graphs, max flow |
A - Assigning Teams
Resolva este problema: URI
Um exemplo de implementação segue abaixo:
B - Back to the Future
Resolva este problema: URI
Um exemplo de implementação segue abaixo:
C - Counting Self-Rotating Subsets
Resolva este problema: URI
É trivial calcular a resposta quando o tamanho do subconjunto é \(1\), existem \(N\) conjuntos de tamanho \(1\) e todos são auto-rotativos. Podemos nos focar então apenas conjuntos com pelo menos dois pontos. Considere um conjunto auto-rotativo com centro \(C\) e ângulo \(A\). Seja \(P\) um ponto no conjunto diferente de \(C\). Seja \(P_1 = P\) e \(P_{i+1}\) obtido a partir da rotação de \(P_i\). Como o conjunto de pontos é finito, para algum par \((i, j)\) temos \(P_i\ =\ P_j\). Além disso, como podemos rotacionar \(P_i\) no sentido contrário \(i-1\) vezes para obter \(P\), \(P_{j-i+1}\ =\ P_1\ = P\). Assim, \(P_1\), \(P_2\), \(\dots\), \(P_{j-i}\) estão todos no conjunto e são os vértices de um polígono regular (ou um polígono regular degenerado se \(j - i = 2\).
O único polígono regular com vértices em coordenadas inteiras é o quadrado (uma possível prova é descrita aqui). Assim, os possíveis ângulos de rotação são 90, 180 e 270 graus. Se um conjunto é auto-rotatório com 90 ou 270 graus, também é auto-rotatório com 180 graus, então precisamos apenas considerar 180. Um conjunto é auto-rotativo com 180 graus se for simétrico no centro de rotação. Assim, um conjunto auto-rotativo deve ser formado por pontos que pertencem a pares que compartilham o mesmo ponto médio, o centro é o ponto intermediário de cada par e, além disso, podemos ter o centro no conjunto ou não.
Para resolver o problema, encontramos o centro para cada par de pontos no conjunto de entrada. Para cada ponto médio, se houver \(K\) pares coincidindo lá, ele contribui com \(\binom{2K}{2T}\) subconjuntos de tamanho \(2T\) e também com \(\binom{2K}{2T}\) subconjuntos de tamanho \(2T +1\) se o centro também é um ponto no conjunto, para \(T\) entre \(1\) e \(K\).
Se precalculamos os fatoriais entre \(1\) e \(N^2\) e seus inversos modulo \(10^9 + 7\) e usarmos uma estrutura de dados como o std::map do C++ para agregar os pares que compartilham o ponto médio a complexidade total da solução fica \(O(N^2 \log N)\).
D - Dating On-Line
Resolva este problema: URI
Um exemplo de implementação segue abaixo:
F - Farm robot
Resolva este problema: URI
Um exemplo de implementação segue abaixo:
G - Game of Matchings
Resolva este problema: URI
Um exemplo de implementação segue abaixo:
H - Hotel Rewards
Resolva este problema: URI
Um exemplo de implementação segue abaixo:
I - Internet Trouble
Resolva este problema: URI
J - Just in Time
Resolva este problema: URI
Um exemplo de implementação segue abaixo:
K - Kill the Werewolf
Resolva este problema: URI
Um exemplo de implementação segue abaixo: