Alguns problemas no BOCA requerem técnicas ou estruturas de dados mais avançadas. Este post tem como objetivo discutir e auxiliar na resolução destes problemas. Fiquem atentos, sempre que possível estaremos atualizando esse post com novas dicas e soluções.
Problemas discutidos:
| Problema | Dificuldade | Técnica relacionada |
|---|---|---|
| Rain Fall | 4 | matemática |
| Artskjid | 4 | programação dinâmica |
| Hungry Fox | 5 | ad hoc |
| Solar flight | 7 | geometria + segment tree |
| Code Permutations | 7 | programação dinâmica + combinatória |
| O Convidado | 7 | DFS + Sqrt-decomposition |
| Festa de aniversario | ? | ? |
Rain Fall
A chuva é recolhida num tubo transparente vertical com marcas milimétricas, e uma vez que a chuva parou de cair, pode-se verificar a altura da água no tubo. O problema informa que esse tubo tem um vazamento na altura L. Se o nível da água estiver acima de L a água drena do tubo a uma taxa de K mm/h. O objetivo é descobrir qual a quantidade de chuva capitada pelo o tudo durante um certo período.
O primeiro passo é observar que existem três casos possíveis em relação aos valores fornecidos na entrada: I) H < L nesse caso a resposta deve ser H H visto que se H < L não ocorreu vazamento durante o período que choveu, logo o volume mínimo e máximo é H; II) H = L nesse caso a resposta é dada por L C uma vez que podemos supor que a vazão do vazamento foi igual a taxa de chuva, logo a quantidade mínima de chuva possível é L. O volume máximo, representado por C, devemos calcular; III) H > L nesse caso a resposta correta seria C C .
O segundo passo é computador o valor de C. Note-se que se descobrirmos a taxa de chuva, uma vez que o problema não informa esse valor mas afirma que é constante, podemos calcular o valor de C. Seja R a taxa de chuva ao longo do período fornecido, então:
C = R*T₁
A Figura abaixo ilustra um exemplo do problema fornecido no enunciado.
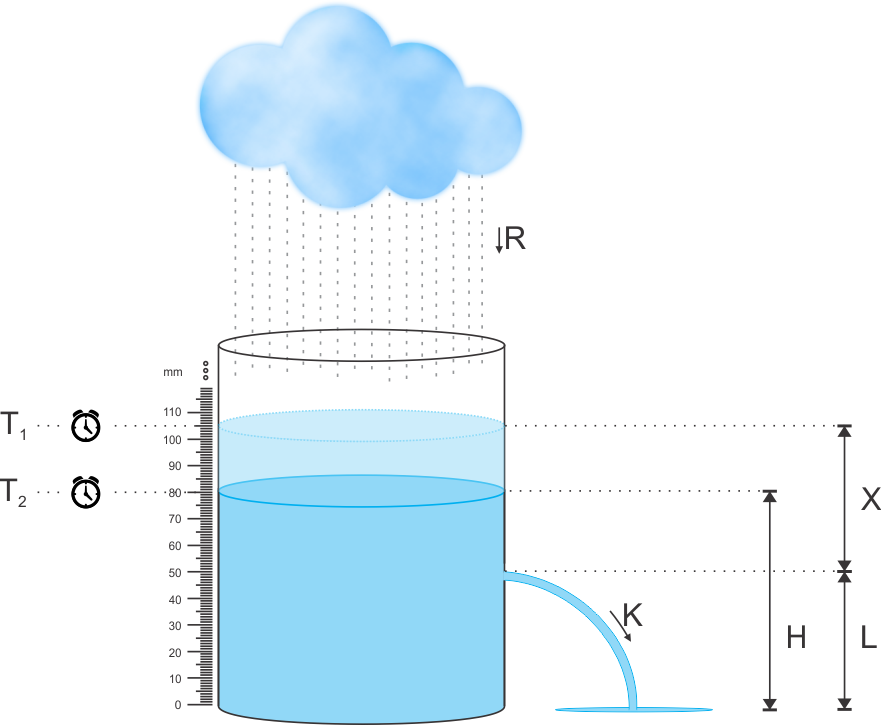
O volume máximo de chuva, C, seguindo a Figura acima, é dado por:
C = X + L
O valor de X, por sua vez, pode ser encontrado como segue:
X = (R-K)*(T₁ - L⁄R)
Portanto,
C = (R-K)*(T₁ - L⁄R) + L
Por outro lado, sabemos que o volume observado mais a quantidade de água vazada também nos dá o volume máximo de chuva, visto que a água não evapora. Esse volume é dado por:
H + k* T₂
Logo, esses volumes devem ser iguais:
(R-K)*(T₁ - L⁄R) + L = H + k* T₂
Para descobrir a taxa de chuva basta isolar o vaor de R , nesse processo ( fica como exercício ) chegamos em:
R2 * T₁ + R * (- T₁ * K - H - K * T₂) + K * L = 0
Chegamos em uma equação do segundo grau, basta aplicarmos Bhaskara e descobrir o valor de R.
O convidado
O problema consiste em dado uma árvore e os valores inteiros associados a cada nó da mesma, o seu programa deverá ser capaz de processar dois tipos de consultas:
- Tipo 1: dados i e j, fazer a atribuição x[i] = y;
- Tipo 2: dados i e y, imprimir a quantidade M de vértices da subárvore de i que tenha valor x[j] ≤ y, onde o vértice j pertence à subárvore de i.
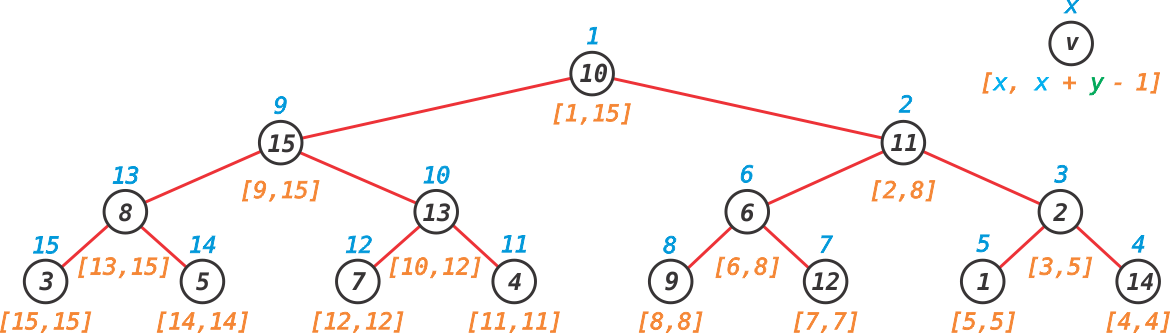
A solução mais intuitiva é responder a consulta do Tipo 1 em O(1) e realizar um DFS/BFS para responder a constulta do Tipo 2. Essa última será respondinda em O(Q*N), onde Q representa a quantidade de consultas. Como Q*N ≤ 1010 essa solução não vai passar no tempo limite de 3 segundos. Portanto, como responder a segunda consulta de forma eficiente? O primeiro passo é linearizar a árvore fornecida realizando um percurso em profundidade nela. À título de exemplo, suponha uma árvore com N = 15 nós, representada na Figura abiaxo.
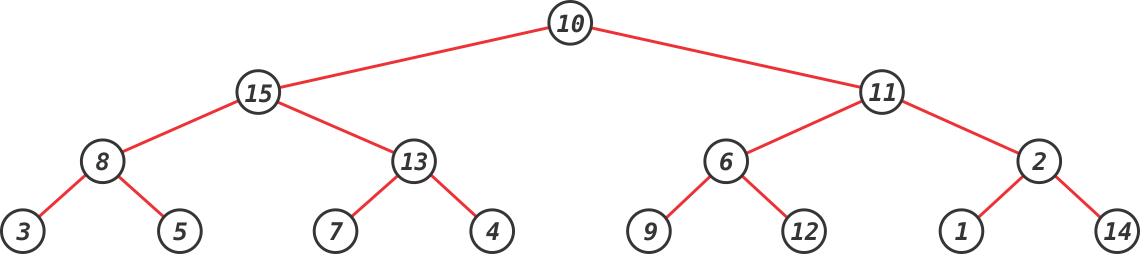
O processo de linearização é ilustrado na Figura abaixo. Note que cada nó v da árvore agora é mapeado para um valor x , esse valor é o tempo de descoberta do nó.
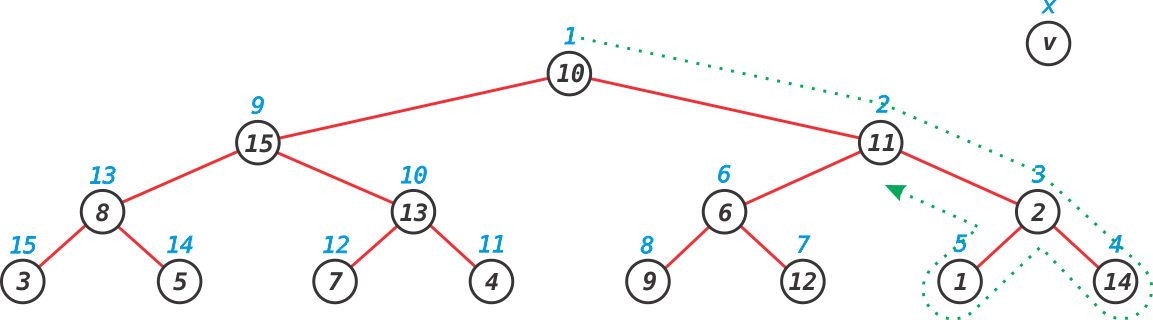
Aproveitando o percurso em profundidade, vamos armazenar também o tamanho da subárvore de cada nó da árvore. Essa quantidade é representada por y na Figura a seguir.
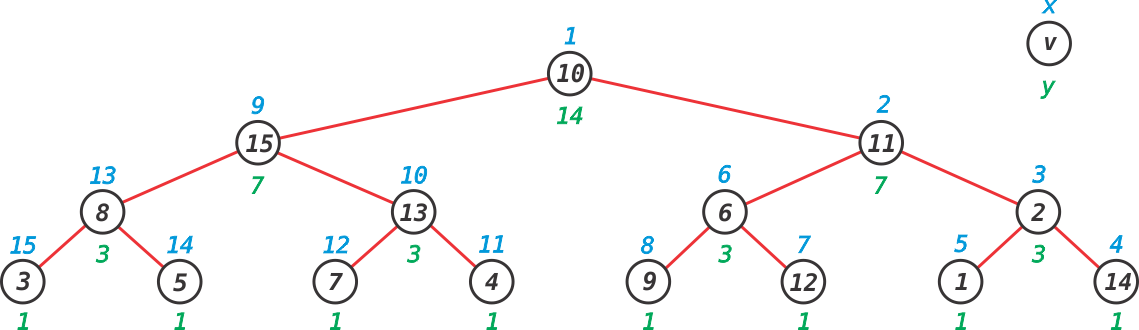
Com o mapeamento e a quantidade de nós na subárvore de cada nó calculados, podemos representar uma subárvore de um nó v como um intervalo. Por exemplo, o nó 11 foi mapeado para x [ 11 ] = 2 e contém y [ 11 ] = 7 nós na sua subárvore. Portanto, o intervalo [ x[ 11 ], x[ 11 ] + y[ 11 ] - 1 ] = [ 2, 2 + 7 - 1 ] = [ 2, 8 ] pode representar tal subárvore. O restante dos intervalos são mostrados na Figura abaixo. Note-se que cada intervalo é definido em cima do mapeamento reaizado, ou seja, não estão relacionados diretamente com o número do nó em si, mas sim com o valor do seu mapeamento.
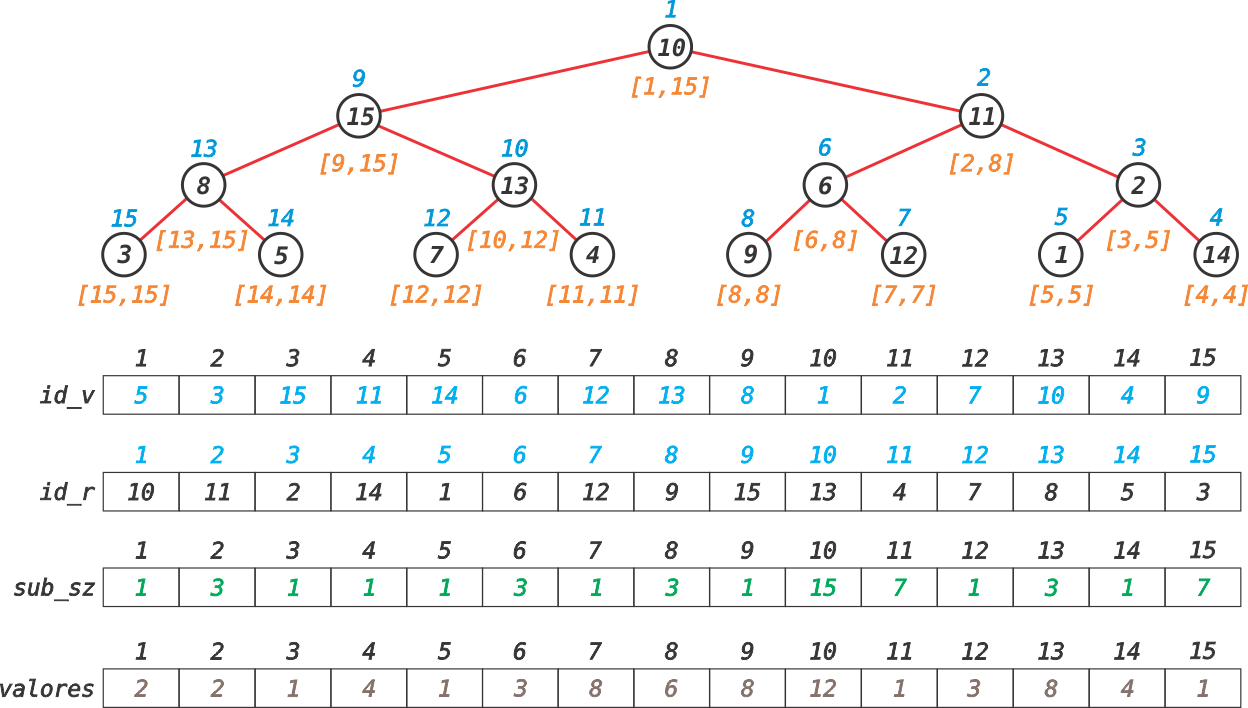
O valores calculados até então podem ser armazenados em vetores:
- id_v : armazena os valores dos mapeamentos x;
- id_r : armazena o mapeamento reverso dos nós, ou seja, se id_v[ v ] = w então id_r[ w ] = v;
- sub_sz : armazena os tamanhos das subárvores de cada nó mapeado y;
A Figura abaixo ilustra tais vetores.
Como a árvore linearizada e "dividida" em intervalos, podemos utilizar a técnica SQRT-Decomposition para responder a consulta do Tipo 2 em O(Q*(N/√N + √N * lg( N/√N))). Essa técnica é relativamente simples de ser compreendida e deixo como exercício.
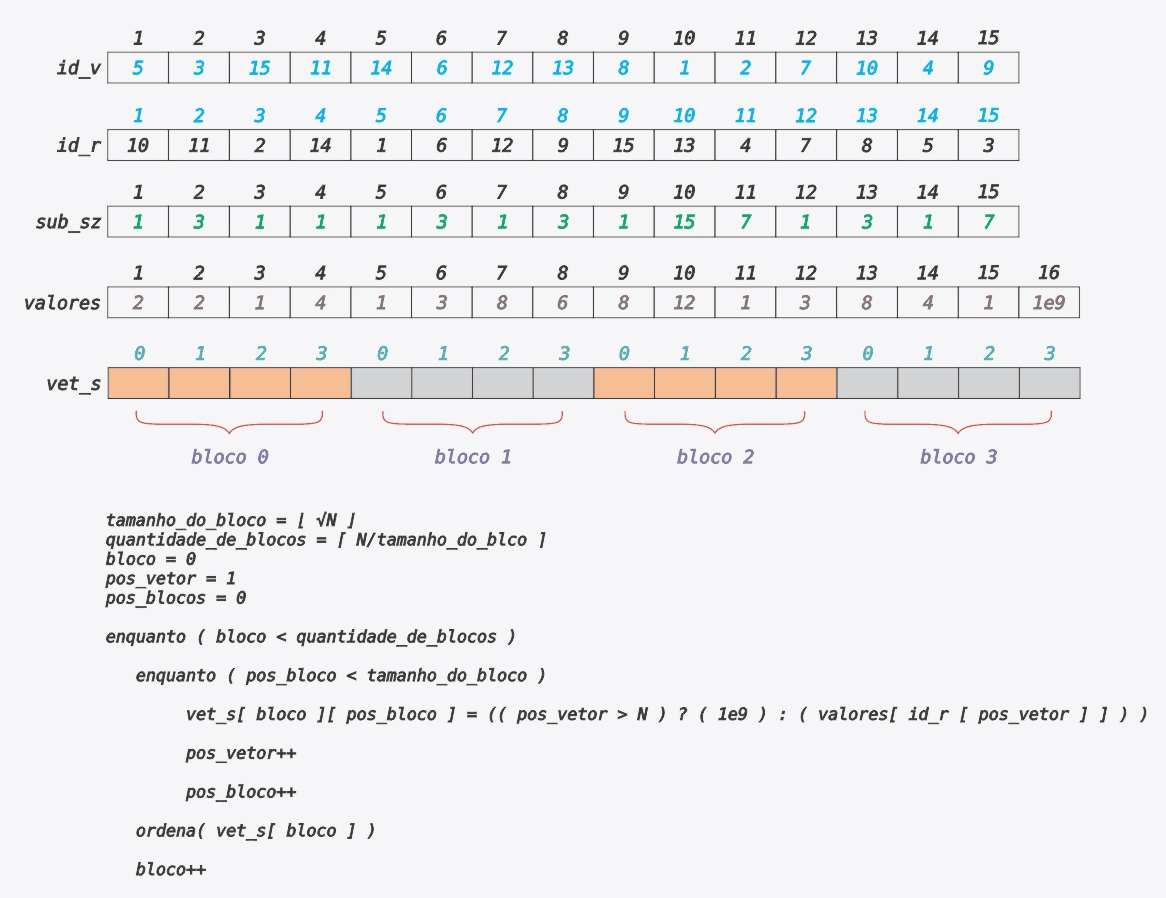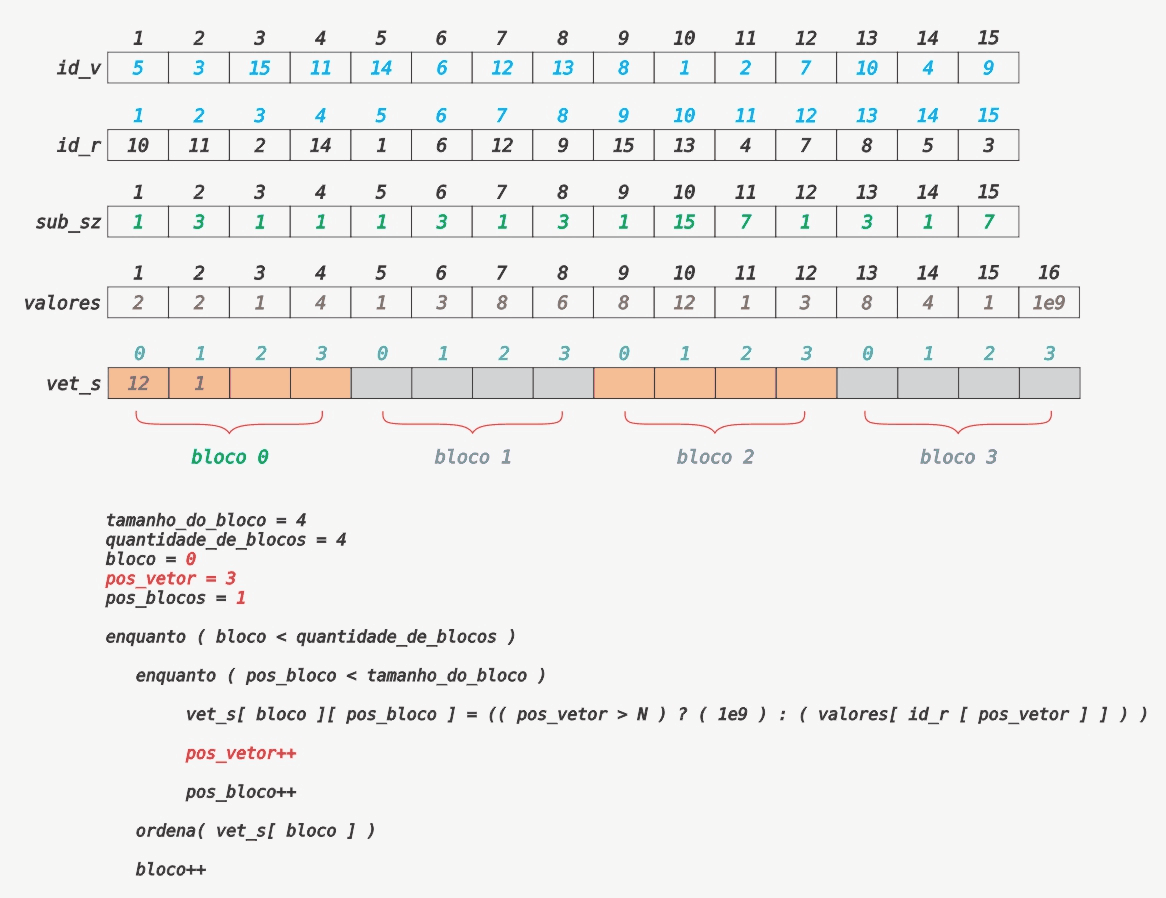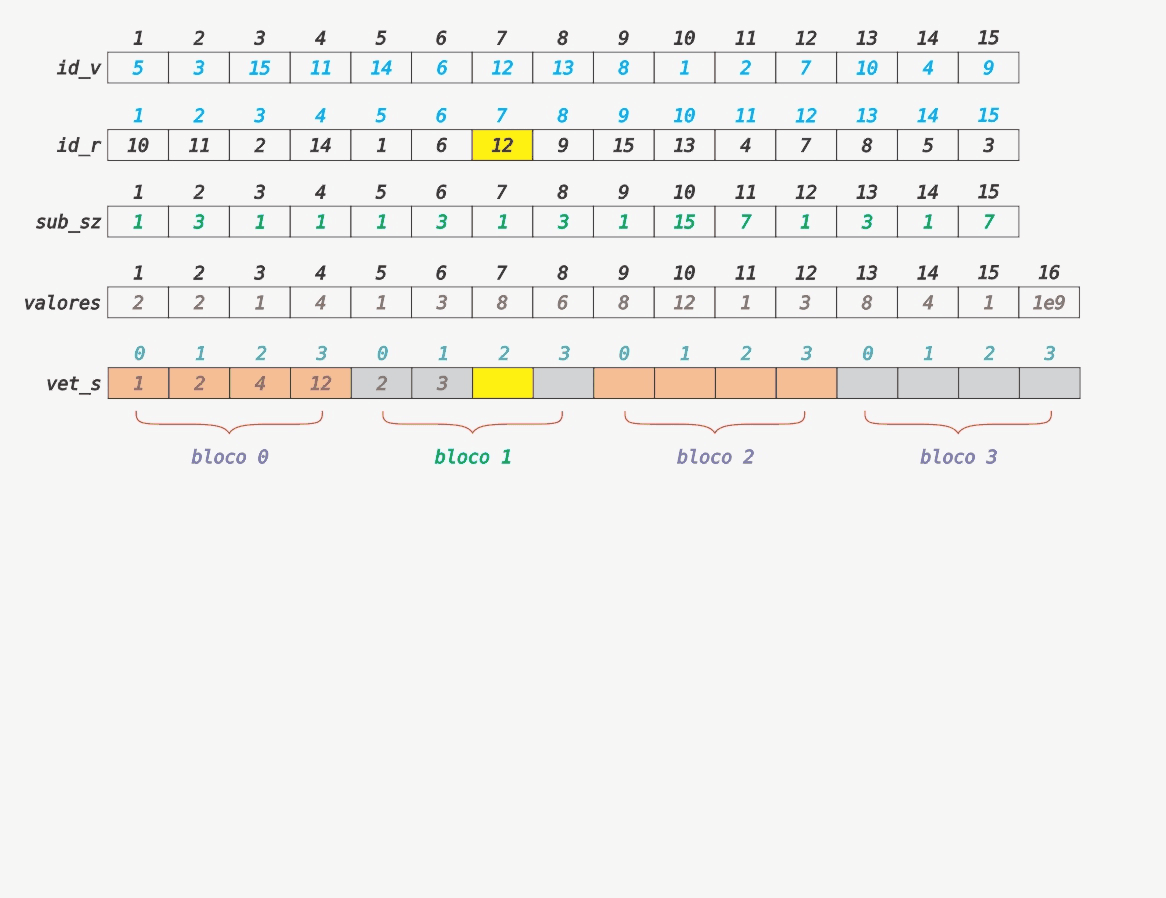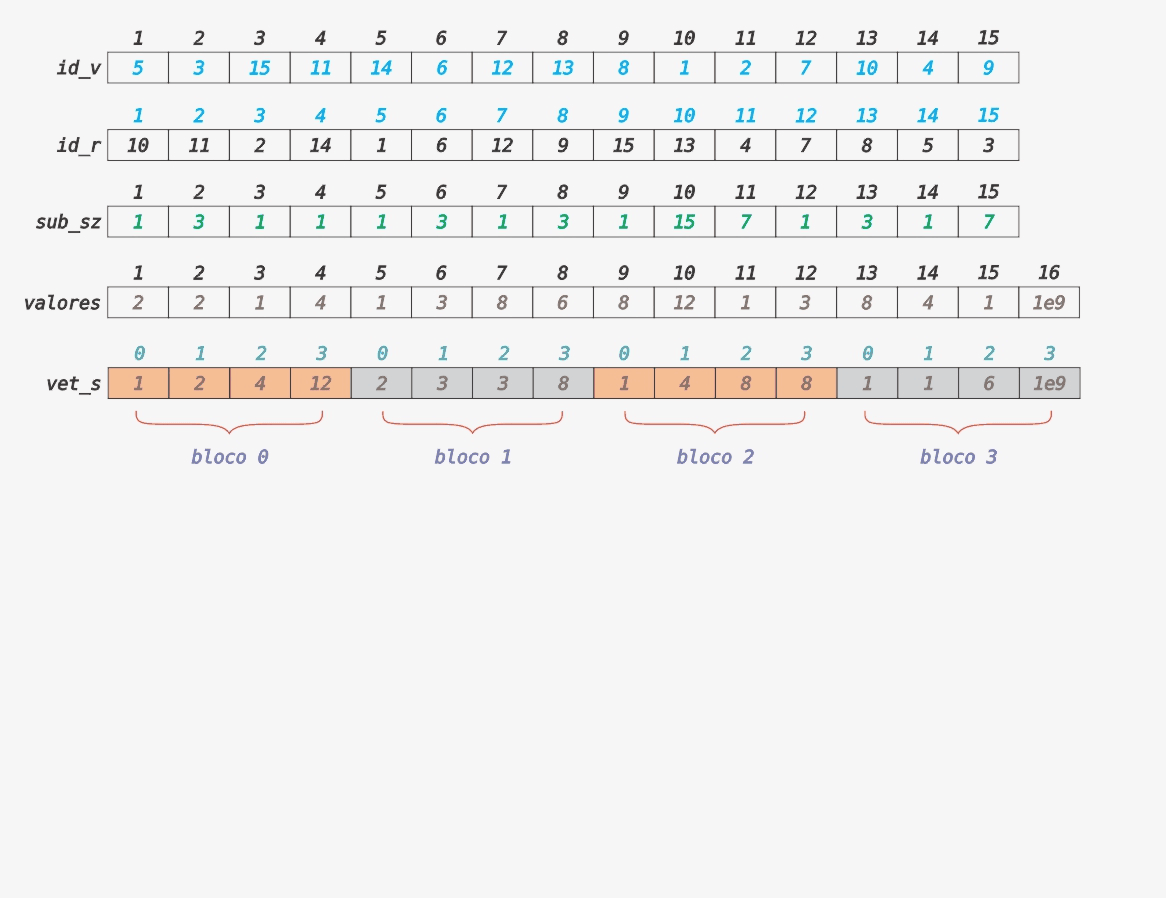
O valor de ⌊√15⌋ = 3, note-se que 15 é divisível por 3. Como N pode não ser divisível por ⌊√15⌋, então vamos considerar, para esse exemplo, o tamanho do bloco igual a 4 para que possamos mostrar como tratar tal caso. Para acessar o bloco correto, dado um nó, basta realizar a seguinte operação de divião ⌊(id_v[ no ] - 1) / 4⌋. Já a posição dentro do bloco, basta descobrir o resto da divisão (id_v[ no ] - 1) % 4. Quando o valor de ⌊√15⌋ não dividir N, basta completar o último bloco com um valor bem alto, por exemplo 1e9, desta forma esses valores não vão influênciar na resposta.
Seja vet_s uma matriz com ⌈N/⌊√15⌋⌉ linhas e ⌊√15⌋ colunas que armazena os valores de cada nó em blocos. Perceba que estamos considerando o tamanho do bloco igual a 4, logo vet_s terá ⌈15/4⌉ = 4 linhas e 4 colunas. O próximo passo é ordenar cada bloco/linha dessa matriz. Para simplificar as islustrações a seguir, considere que cada bloco/linha da matriz vet_s foi concatenada uma na frente da outra, formando um vetor. O Gif a seguir ilustra a matriz vet_s e o processo de preenchimento da mesma.
Consulta do Tipo 1
Vamos supor a seguinte consulta do Tipo 1, atualizar ( no, valor_antigo, valor_novo ), uma atualização do valor do nó no com o valor valor_novo, o valor_antigo é o valor atual do nó, ou seja, valores[ no ]. Seja i o índice do bloco do nó no e j a posição dentro desse bloco. A objeitvo é autalizar o vetor valores e a matriz vet_s. O primeiro é alcançado fazendo a seguinte atribuição valores[ no ] = valor_novo, já o segundo devemos encontrar o valor valor_antigo dentro do bloco, uma busca linear no bloco então e realizado. Encontrado um valor valor_antigo, basta atualiza-lo com o valor valor_no. Devemos manter o bloco ordenado para que a consulta do Tipo 2 possa ser realizada corretamente. Nesse ponto, após a troca, três casos podem ocorrer:
- O valor da posição j-1 é maior que o valor_novo: nesse caso basta trocar o valor de vet_s[ i ][ j ] com vet_s[ i ][ j - 1 ], então o valor de j deve ser decrementado e o processo é repetido enquanto j-1 ≥ 0 e vet_s[ i ][ j-1 ] > vet_s[ i ][ j ]
- O valor da posição j+1 é menor que o valor_novo: nesse caso basta trocar o valor de vet_s[ i ][ j ] com vet_s[ i ][ j + 1 ], então o valor de j deve ser incrementado e o processo é repetido enquanto j+1 ≤ 4 e vet_s[ i ][ j + 1 ] < vet_s[ i ][ j ]
- Se nenhum dos casos anteriores forem sastifeitos: nesse caso não será necessário deslocar o valor_novo, visto que o bloco já está ordenado.
Um exemplo dos passos da atualização é mostrado no Figura abaixo.

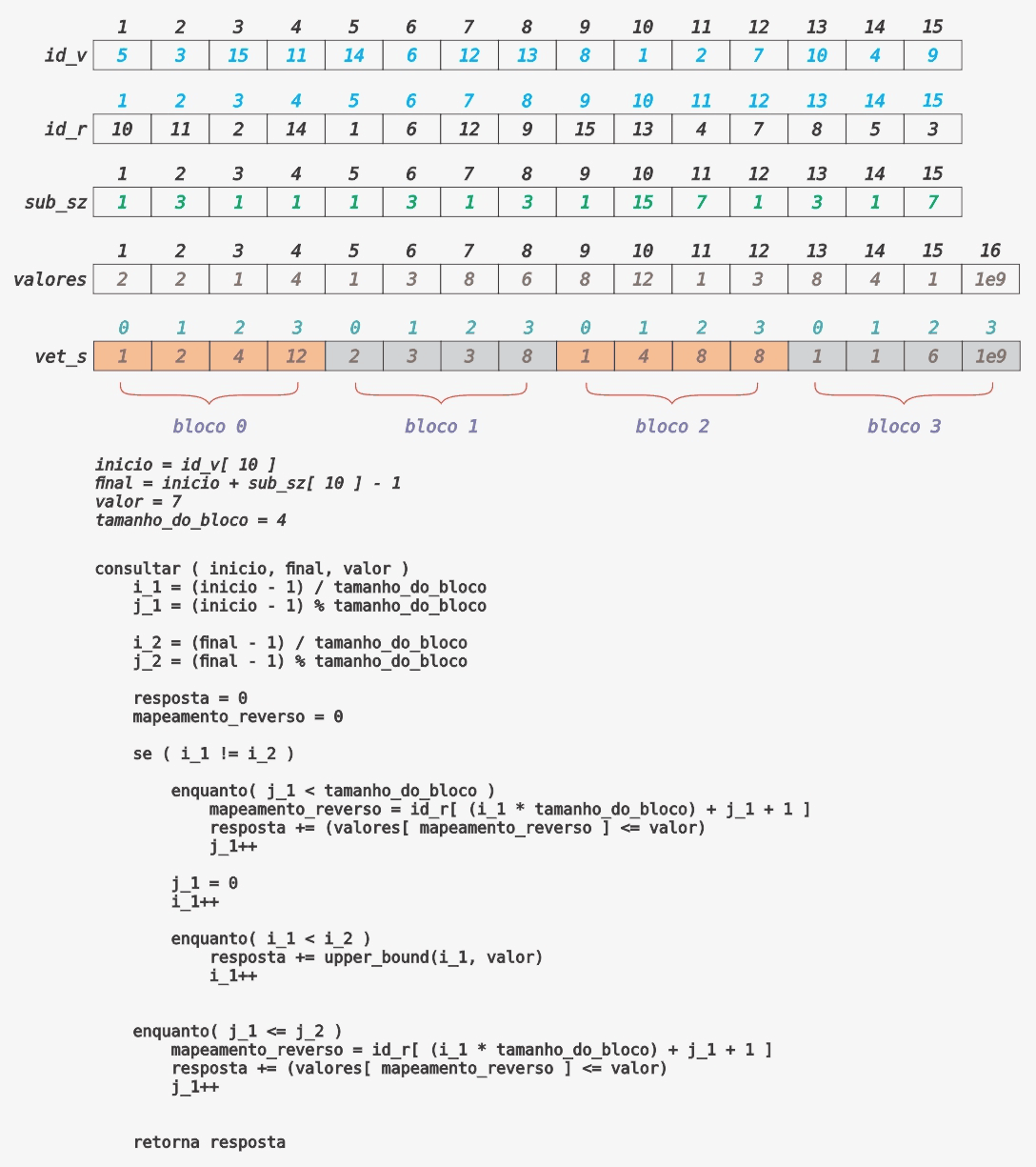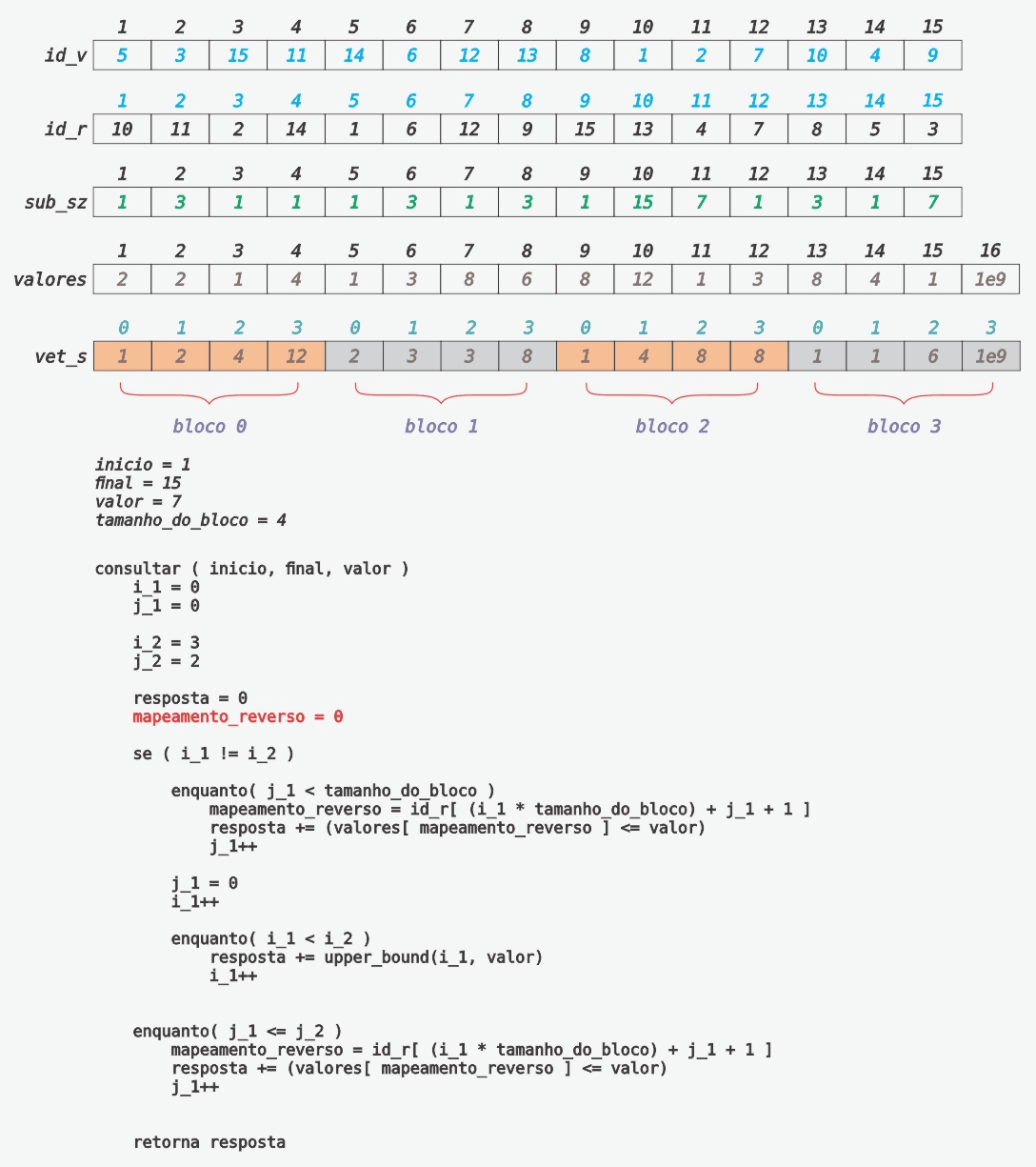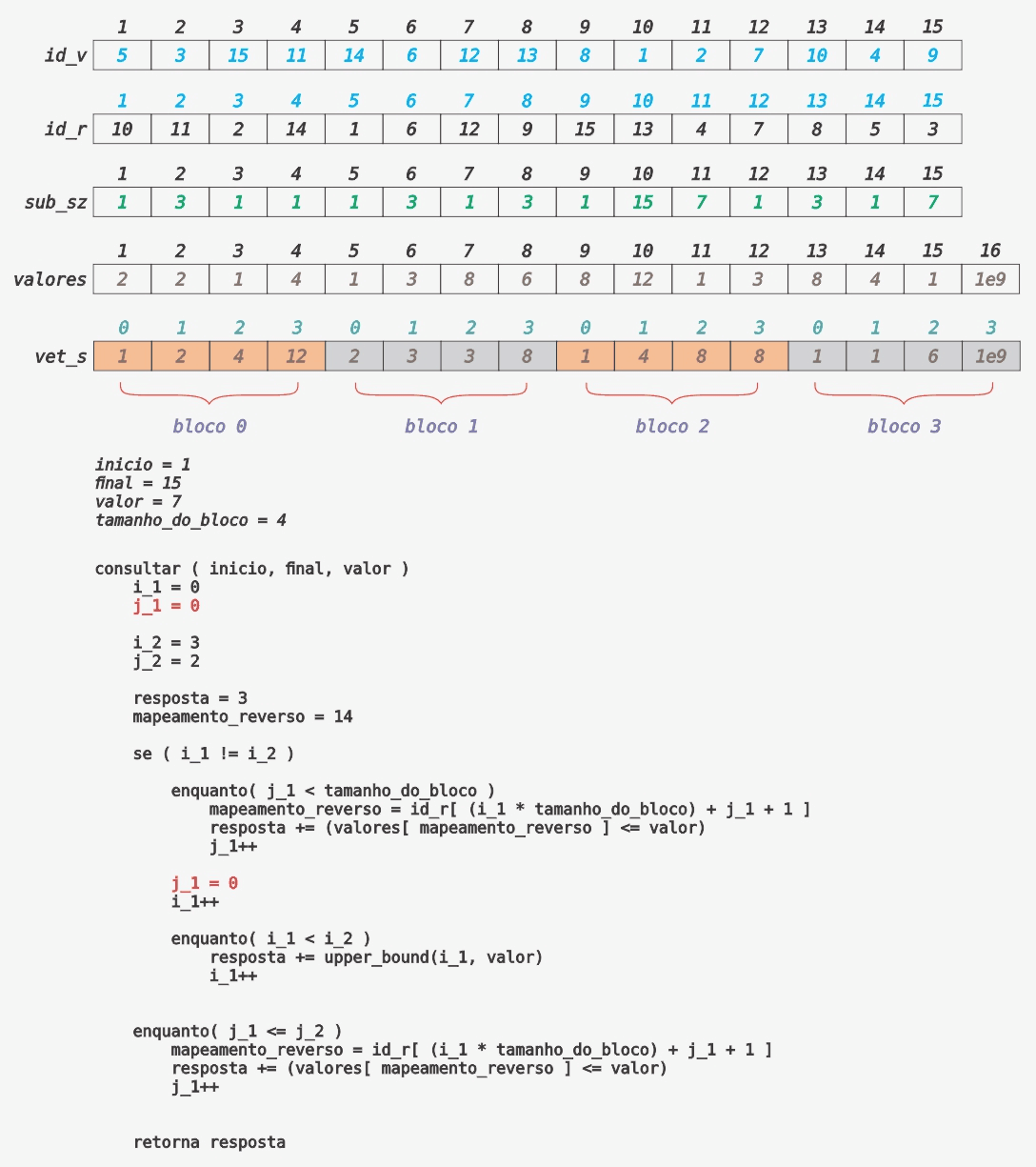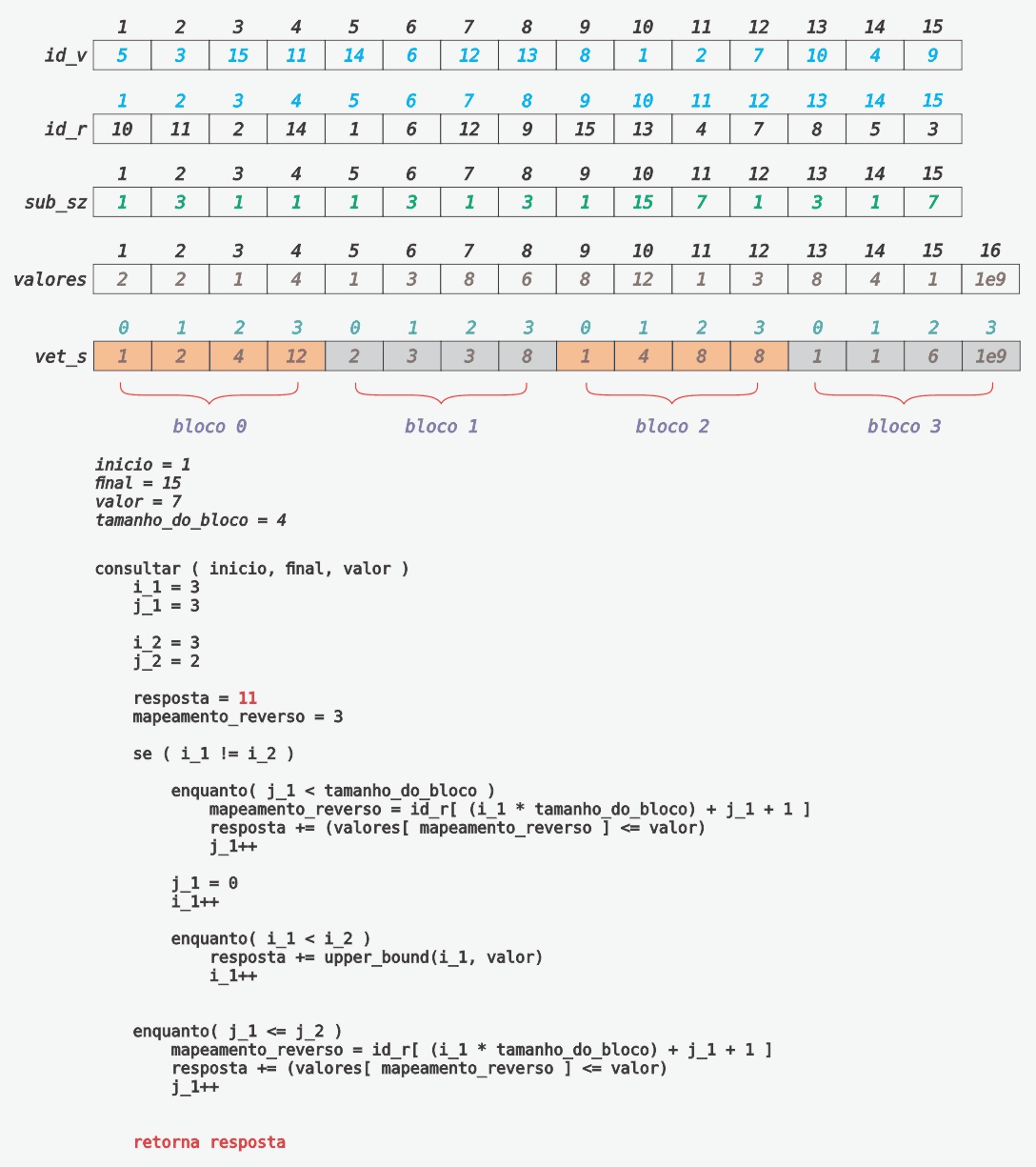
Consulta do Tipo 2