TAP-2018/1 - Treino 1

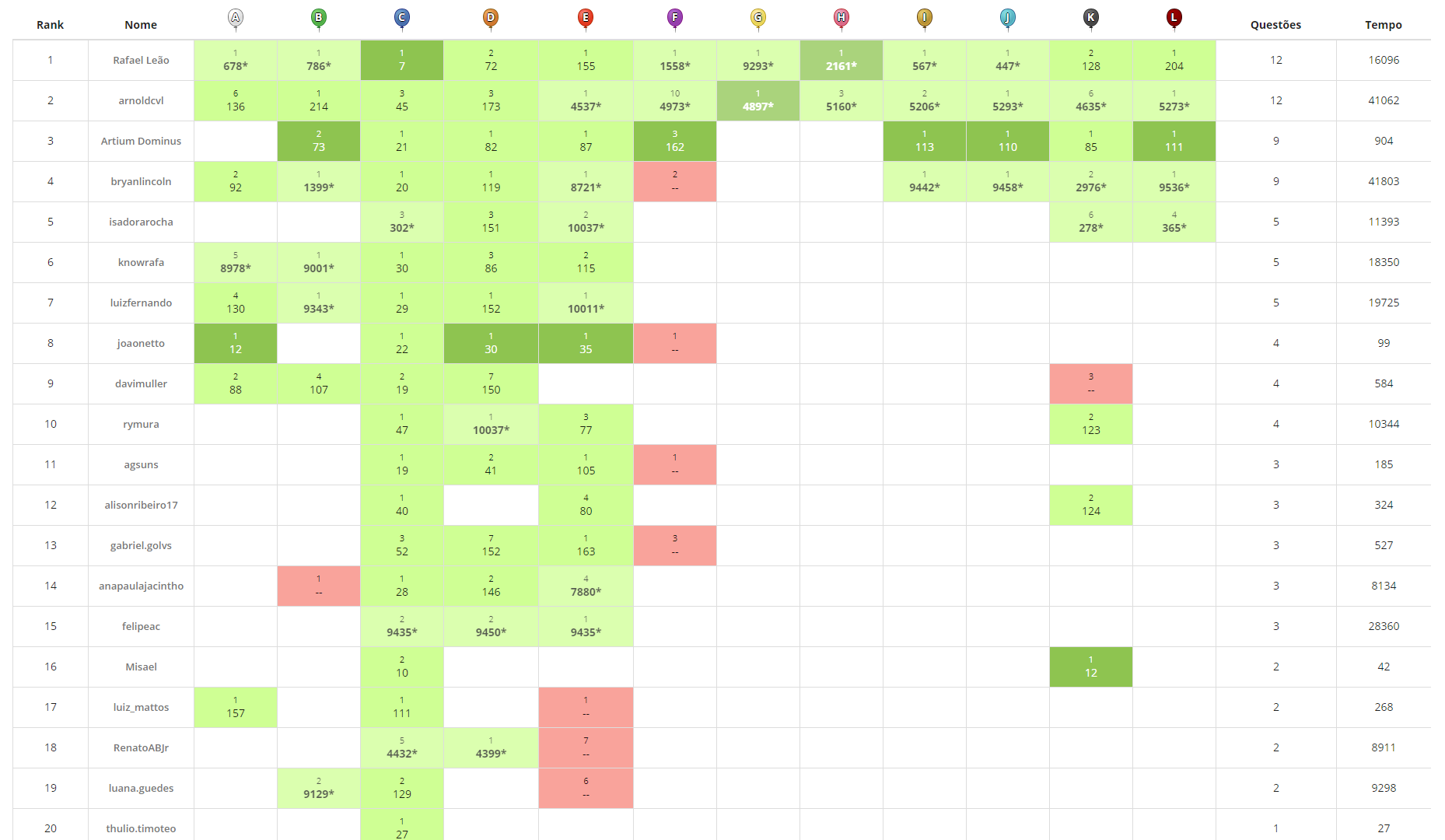
Aconteceu em 14 de Março de 2018 o primeiro treino da disciplina TAP - Tópicos Avançados de Programação. O placar final do treino pode ser visto na imagem abaixo.

A prova foi composta por 13 problemas. Os níveis dos problemas e as respectivas técnicas que podem ser usadas para resolve-los é apresentado na tabela abaixo.

Problema	Dificuldade	Técnica relacionada
A - Bingo!	3	ad hoc
B - Horas e Minutos	2	ad hoc
C - LED	1	string
D - Árvore de Natal	2	ad hoc, substr
E - Telefone Sem Fio	2	contadores
F - Trilhos	3	pilha
G - Diamantes e Areia	2	contadores, pilha
H - Pontos de Feno	3	mapas, STL maps
I - Dama	1	ad hoc
J - Mapa do Meistre	2	travessia em grafos
K - Flores de Fogo	2	geometria
L - Primo Rápido	2	matemática
M - Guarda Costeira	2	matemática, Ad Hoc

A - Bingo!

Resolva este problema: URI

O enunciado do problema começa explicando a versão clássica do jogo de Bingo e logo após apresenta uma nova versão chamada Albert-Charles-Mary. Nesta versão o caller sorteia uma primeira bola, coloca-a de volta no globo, sorteia uma segunda bola, coloca-a de volta no globo e então anuncia a diferença absoluta entre os números das duas bolas. O problema consiste em descobrir se é possível gerar todos os números de 0 até N através destas diferenças levando em consideração as B bolas que restaram dentro do globo. Seja bi o valor de alguma bola i dentro do globo e c um valor entre 0 e N inclusive, c é gerado se existir alguma bola, dentro do globo, com o valor bi + c. Como o valor de N ≤ 90, podemos olhar para todos os valores possíveis de c, ou seja, de 0 até N e verificar se o valor bi + c está dentro do globo.

Um exemplo de implementação segue abaixo:

B - Horas e Minutos

Resolva este problema: URI

O maior e menor ângulo obtidos pelos os dois ponteiros são 0 e 180, respectivamente. A quantidade de marcas, entres os ponteiros, quando apresenta o ângulo 180 pode ser observado na figura do relógio fornecida no enunciado. Note-se que são 6*5 = 30 marcas, portanto o intervalo entre duas marcas consecutivas tem 180/30 = 6 graus. Então um ângulo é gerado se for um múltiplo de 6.

Um exemplo de implementação segue abaixo:

C - LED

Resolva este problema: URI

Basta contar a quantidade de leds utilizados por cada letra.

Um exemplo de implementação segue abaixo:

D - Árvore de Natal

Resolva este problema: URI

Implementação...

Um exemplo de implementação segue abaixo:

E - Telefone Sem Fio!

Resolva este problema: URI

O enunciado começa explicado como funciona a brincadeira do “telefone sem fio” com dois times. Nesse problema, devemos nos atentar aos critérios de desempate:

“A equipe vencedora é aquela cuja frase final seja mais próxima da frase original. Para calcular a semelhança entre duas frases de mesmo comprimento você deve contar o número de vezes em que o caractere da frase do time coincide com o caractere da frase original. Ganha o time para o qual o número de coincidências seja máximo. Se os dois times empataram neste critério, a primeira vez que um dos times acertou e o outro errou decide.”

Seja FO, F1 e F2 a frase original, a do primeiro e segundo time, respectivamente. Vamos percorrer a frase original, da esquerda para a direita, e comparar o caractere da posição atual com o caractere das fases dos times na mesma posição. Os quatros casos a seguir podem ocorrer ao compararmos: I) os caracteres são iguais; II) apenas o caractere da frase do primeiro time difere do original; III) apenas o caractere da frase do segundo time difere do original; IV) ambos os caracteres diferem do original;

Apenas os I,II e III interferem na pontuação dos times. No caso I ambos recebem um ponto. No caso II, apenas o segundo time recebe um ponto e no caso III o primeiro é que recebe um ponto. Note-se que o critério de desempate leva em consideração a primeira ocorrência do caso II ou III. Portanto, se após percorrer a frase original e os times apresentam a mesma pontuação, basta verificar qual dos casos, II e III, ocorreu primeiro. Se for o caso II então o time 2 ganha, caso contrário o time 1 ganha. No entanto, se as pontuações dos times diferem, então o time que tiver a maior pontuação vence.

Um exemplo de implementação segue abaixo:

F - Trilhos

Resolva este problema: URI

Para cada comboio que chega da direção A continua na direção B com os vagões, reorganizados, de alguma forma. A ordem que esses vagões chegam é sempre crescente 1,2,...,N. Se um vagão entra na estação, ele só pode sair dela caso não tenha outro vagão na sua frente. A única direção que um vagão, posicionado na estação, pode ir é para a direção B. Então dado uma sequência de vagões, o problema pede para verificar se é possível reproduzir tal sequência. Observe que a estação funciona como se fosse uma pilha de vagões, pois o último vagão que chega é o primeiro a sair, vamos denotar essa pilha de vagões por P. A sequência dada pode ser vista como uma fila de vagões, visto que devemos respeitar a ordem da sequência, vamos denota-la por F .

Um comboio consiste de N vagões, para cada um deles, de 1 até N , verifique se o primeiro vagão em F é igual ao vagão que chegou, se for então o vagão segue na direção B e removemos o primeiro vagão de F. Caso contrário, verifique se existe algum vagão na estação, pois o mesmo pode ser o vagão que deveria sair agora. Se for então remova-o do topo de P e também remova o primeiro vagão de F. Se não for o vagão que deveria sair agora, então empilhe o vagão recém chegado em P.

Após a chegada de todos os vagões, a sequência fornecida é alcançável se P e F estiverem vazias, pois não sobrou nenhum vagão na estação e a fila de vagões que saíram na direção B foi respeitada, portanto saída deve ser Yes. Caso contrário, a sequência não é alcançável e a saída deve ser No.

Um exemplo de implementação segue abaixo:

G - Diamantes e Areia

Resolva este problema: URI

O problema pede para encontrar a quantidade de diamantes que compõem uma entrada. A entrada é composta por três tipos de caracteres: <, > e .. Um diamante é formado por dois caracteres: < >. Observe que as partículas de areia, ., não interfere na formação de diamantes. Portanto, para cada caractere < verificamos se o próximo caractere, ignorando os ., é um >. Se for encontramos um diamante, o próximo passo consiste em remover esses dois caracteres. Vamos repetir esse processo até não encontramos mais nenhum diamante. A complexidade dessa abordagem é O(N²), corre o risco de não ser aceita dependendo do servidor onde o problema é está sendo executado.

Uma outra abordagem, com complexidade O(N), consiste em computar a quantidade de diamantes em uma única passada na string de entrada. Vamos criar dois contadores, aberto e diamantes que armazenam a quantidade de caracteres do tipo < e a quantidade de diamantes encontrados até o momento, respectivamente. Então, para cada caractere, da esquerda para a direita, verificamos se é do tipo <, se for então aberto = aberto + 1, se for do tipo . não fazemos nada, caso seja do tipo > verificamos se aberto > 0 , se for então um novo diamante pode ser formado, logo diamantes = diamantes + 1. Como utilizamos um < combinado com o > atual, devemos decrementar a quantidade de caracteres do tipo <, sendo assim aberto = aberto - 1.

Após processamos todos os caracteres a resposta está armazenada em diamantes. Note-se que esse problema também pode ser resolvido substituindo a variável aberto pela estrutura de dados pilha. Caso não esteja familiarizado fica como um exercício ;D.

Um exemplo de implementação segue abaixo:

H - Pontos de Feno

Resolva este problema: URI

O problema lhe fornece um dicionário Hay Point que contém algumas palavras-chaves e um valor, em dólares americanos, associado a cada uma dessas palavras-chaves. O salário de um funcionário é calculado através da soma do valor de todas as palavras que aparecem na descrição do cargo deste funcionário. O problema pede que você compute, para cada funcionário, o valor deste salário. Esse problema é um excelente reposta para a pergunta: “OK! Aprendi como utilizar Map da STL, mas qual problema eu posso praticar?” O contêiner Map da STL , em suma, são contêineres associativos que armazenam elementos de forma mapeada. Cada elemento tem um valor de chave e um valor mapeado. Não existem dois valores mapeados que tenham os mesmos valores de chave.

Seja M<string,int> um Map composto pela chave e valor do tipo string e int, respectivamente, e S uma variável que irá armazena o salário do funcionário. O primeiro passo é inserir todas as palavras-chaves do dicionário e seus respectivos valores em M. O passo seguinte consiste em, para cada palavra da descrição caso a mesma esteja em M, somar o valor associado em S: S = S + M[ palavra ]. Após processar uma descrição da entrada, basta imprimir o valor de S.

“Certo, mas se eu não programo em C++ devo pular esse problema?” Não meu(minha) jovem. Em Java temos o HashMap. “Mas em C ?” Nesse caso é quando você chora e a mãe não ouve =). Brincadeiras à parte, as seguintes abordagens, independente da linguagem, podem ser implementadas:

Força bruta: os valores N, M e K são pequenos, K representa o tamanho da palavra. Portanto uma abordagem com complexidade O(N*M*K) é aceita. Nesta abordagem, podemos armazenar cada palavra-chave em um vetor e para cada palavra da descrição fazemos uma busca linear nesse vetor, se encontrarmos a palavra no vetor adicionamos à S o valor dela, caso contrário adicionámos o valor 0.

Busca binária: podemos diminuir a complexidade da abordagem anterior se ordenarmos o vetor com as palavras-chaves e ao invés da busca linear, aplicarmos uma busca binária.

Árvore Trie: a Trie é uma estrutura de dados de recuperação rápida: retrieval. A complexidade de inserção, remoção e pesquisa são todos na ordem de O(K). Portanto, podemos inserir todas as palavras-chaves em uma Trie com complexidade O(N*K) e para cada palavra da descrição pesquisamos se a mesma está presente na Trie, se estiver adicionamos o valor desta palavra à S. A complexidade final com a Trie fica em O((N*K) + (M*K)).

Um exemplo de implementação segue abaixo:

I - Dama

Resolva este problema: URI

O problema lhe fornece a posição de uma rainha e pede a quantidade mínima de movimentos necessários para chegar em outra posição do tabuleiro 8x8. A primeira vista parece um problema de grafos, podemos aplicar uma busca em largura para descobrir a quantidade mínima de movimentos. Essa abordagem é aceita, mas se paramos para analisar o problema em si, percebemos que existem apenas três casos: I) a posição deseja é a mesma que a posição atual; II) a posição deseja é alcançável com um único movimento; III) a rainha consegue cobrir todas posições do tabuleiro com apenas dois movimentos, logo se a posição não é alcançável com 0 e nem com 1 movimento então, com certeza, é com 2 movimentos.

Um exemplo de implementação segue abaixo:

J - Maester’s Map

Resolva este problema: URI

O enunciado do problema pede para fazer um programa para verificar se um mapa leva ou não a um ponto com um baú de obsidiana. Esse problema pode parecer complicado a primeira vista mas é bem simples, basta começar no canto superior esquerdo e seguir as flechas como descrito no enunciado, ou seja, bem direto, basta implementar o que o enunciado informa.

Um exemplo de implementação segue abaixo:

K - Flores de Fogo

Resolva este problema: URI

Dados dois círculos, um desenhado por um ambicioso caçador de flores de fogo e outro representando a área da flor, sua tarefa é determinar se o caçador morre ou fica rico com sua conquista. O caçador morre caso o círculo desenhado por ele não cubra o círculo da flor de fogo. Seja d a distância Euclidiana entre os centros dos dois círculos, o caçador irá morrer se o raio do círculo desenhado por ele é menor que d, ou seja, se d > r1. Caso contrário, o círculo desenhado alcança a flor de fogo, mas o mesmo deve englobar o círculo da mesma. Portanto, se d + r2 > r1 então o círculo desenhado pelo caçador não engloba o círculo da flor, por consequência ele é morto. Caso contrário ele fica rico.

Um exemplo de implementação segue abaixo:

L - Primo Rápido

Resolva este problema: URI

Mariazinha solicita um programa que aceite diversos valores e diga, para cada um destes valores, se são primos ou não. Um valor é primo se tem apenas dois divisores: um e o próprio valor. Como os valores de X < 2147483648 , √X < 46340 e N*√X < 9268000 , podemos procurar um divisor para X, ou seja, precisamos olhar todos os valores até a √X, visto que o maior divisor possível de X é a raiz quadrada do mesmo. X não é primo se nenhum desses valores dividi ele. Caso contrário X é primo.

Um exemplo de implementação segue abaixo:

M - Guarda Costeira

Resolva este problema: URI

A figura abaixo representa a situação apresentada na descrição do problema:

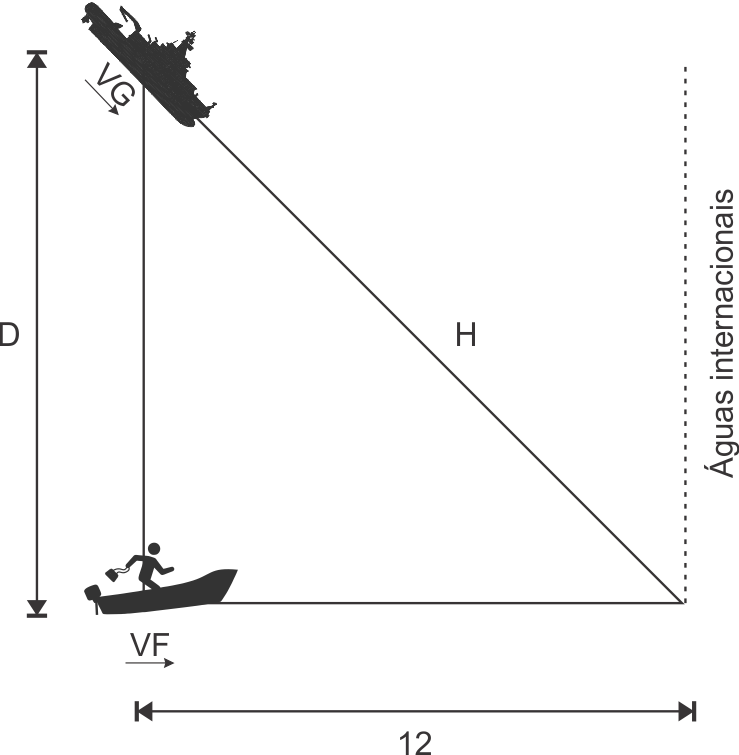
Vamos supor o que a guarda costeira no último instante antes do ladrão conseguir chegar nas águas internacionais. Note-se que esse caso é expresso na Figura acima. Se encontrarmos o valor de H podemos calcular o tempo que a guarda costeira leva para interceptar o ladrão. Esse tempo vai ser TG = ^H⁄_VG. O valor de H pode ser encontrado aplicando o teorema de Pitágoras: H = √( D² + 12² ). O tempo gasto pelo o ladrão vai ser TL = ¹²⁄_VL. Se a guarda costeira chega nas águas internacionais antes ou no mesmo instante que o ladrão, ou seja, TG ≤ TL, então a guarda costeira consegue interceptar o ladrão em algum ponto do seu trajeto em direção às águas internacionais.

Um exemplo de implementação segue abaixo: