Aconteceu em 28 de Março de 2018 o terceiro treino da disciplina TAP - Tópicos Avançados de Programação. O placar final do treino pode ser visto na imagem abaixo.
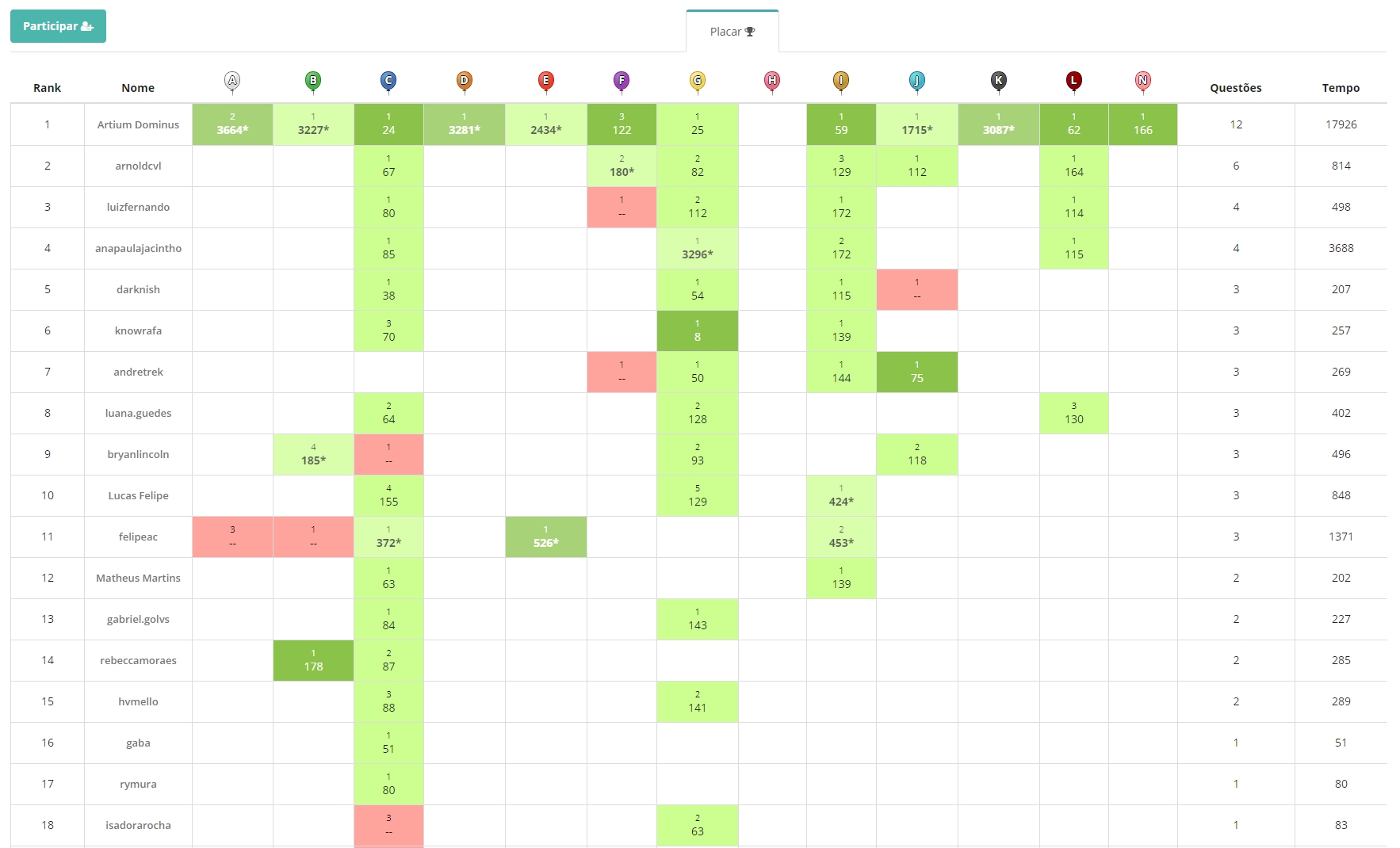
A prova foi composta por 13 problemas. Os níveis dos problemas e as respectivas técnicas que podem ser usadas para resolve-los é apresentado na tabela abaixo.
| Problema | Dificuldade | Técnica relacionada |
|---|---|---|
| A - Abreviações | 3 | map, ad hoc |
| B - Supermarket Line | 1 | priority_queue |
| C - Tradutor do Papai Noel | 2 | map |
| D - Estacionamento Lienar | 2 | stack |
| E - Teclado Quebrado | 1 | list |
| F - Problema Fácil de Rujia Liu? | 1 | vector, array |
| G - Ida à feira | 1 | map |
| H - Gerente de Espaço | 6 | list, map |
| I - Espécies de Madeira | 1 | map |
| J - Pontos de Feno | 1 | map |
| K - Eu Posso Adivinhar a Estrutura de Dados! | 2 | queue, priority_queue, stack |
| L - Jogando Cartas Fora | 2 | queue |
| M - |
7 | segment tree |
| N - Estacionamento | 4 | map |
A - Abreviações
Resolva este problema: URI
O problema pede para que, dado um texto, substitua todas as ocorrências de uma palavra pela sua abreviação. Tal processo é explicado no terceiro paragrafo: “O sistema de abreviações funciona da seguinte maneira: para cada letra, é possível escolher uma palavra que inicia com tal letra e que aparece no post. Uma vez escolhida a palavra, sempre que ela aparecer no post, ela será substituída por sua letra inicial e um ponto, diminuindo assim o número de caracteres impressos na tela”. Segundo o enunciado do probema, o objetivo consiste em abreviar as palavras de forma que o texto fique o mais curto possível. Note que como vamos trocar as palavras por uma letra e um ponto então no final das contas temos nó máximo 26 abreviações possíveis. Uma primeira abordagem seria ordenar as palavras pela critério da maior quantidade de vezes que ocorreram no texto, mas não é garantido que o texto final seja mínimo, pois podem existir palavras maiores que ocorrem uma menor quantidade de vezes mas que minimizam mais o texto se forem abreviadas. Ok! Então basta ordenar as palavras pelo critério do maior tamanho? Não, pois da mesma forma podem existir palavras menores que ocorrem uma quantidade maior de vezes e que minimizam mais no final. O problema destas abordagens é que elas são 8 ou 80, assim a solução é o meio termo delas, ou seja, as palavras que vamos escolher para substituir (quantidade de palavras distintas entre 0 e 26, inclusive) que tenham o maior peso possível: (tamanho_da_palavra - 2) * quantidade_de_vezes_que_tal_palavra_ocorreu_no_texto. Observe o -2 na primeira parte da fórmula, se fosse apenas tamanho_da_palavra * quantidade_de_vezes_que_tal_palavra_ocorreu_no_texto, uma palavra com tamanho 5 que ocorreu 10 vezes teria o mesmo peso que uma palavra de tamanho 10 mas ocorreu 5 vezes. Tal situação permitiria que a primeira palavra fosse escolhida mas o texto seria reduzido por 15 enquanto que escolhendo a segunda palavra o texto seria reduzido por 40, mas por quê? Observe que o tamanho real de um palavra que contribuirá para o peso é o tamanho dela menos 2, já que ela será substituída por uma letra e um ponto.
Um exemplo de implementação segue abaixo:
B - Supermarket
Resolva este problema: URI
O enunciado do problema descreve muito bem o processo de atendimento da fila de clientes. A dúvida pode surgir em como simular a ação do caixa, garantindo que quando o caixa fique livre ele atenda o próximo cliente e se existir dois ou mais caixas que fiquem livre no mesmo tempo, o caixa com menor identificador atenderá primeiro dentre eles. Este é um problema clássico que utiliza fila de prioridade, portanto iremos utilizar uma priority_queue< X >. No caso X será um pair de int’s. O primeiro e o segundo termo de X armazenarão o tempo e o identificador do caixa, respectivamente. O processo é simples, no inicio todos os caixas estão na fila com tempo 0, desta forma o primeiro que irá atender um cliente será aquele com menor identificador. Quando um caixa i começar a atender um cliente j em um tempo t, o mesmo gastará cj * vi unidades de tempo para atende-lo, logo o caixa i ficará disponível novamente no tempo t + cj * vi. O caixa, após atender, entrará novamente na fila. O caixa que estiver na frente da fila de caixas atenderá o cliente i+1. Repita o processo até que todos os clientes tenham sido atendidos. Note que a resposta final é o tempo do último caixa que completou o atendimento de um cliente.
Um exemplo de implementação segue abaixo:
C - Tradutor do Papai Noel
Resolva este problema: URI
Crie um map que armazena o nome do país como chave e a frase de “Feliz Natal” correspondente como valor. Basta ler os nomes dos países e usando a função find verificar se o nome é válido (existe no map). Se existir, imprima a frase correspondente utilizando o nome do país para buscar no map (linha 38). Caso contrário, imprima “— NOT FOUND —” (sem aspas).
Um exemplo de implementação segue abaixo:
D - Estacionamento Linear
Resolva este problema: URI
Este problema pode ser resolvido de várias formas, uma delas é simulando o estacionamento através de uma estrutura de dados stack de frango < X > . Onde X é um pair de int’s. O primeiro e o segundo elementos de X armazenam o tempo que o carro chegou e que deseja sair do estacionamento, respectivamente. A ideia é ir simulando o estacionamento: quando um carro chega, para que seja possível entrar no estacionamento, o tempo de chegada dele tem que ser maior ou igual ao tempo de saída do último carro que entrou no estacionamento. Se tiver algum carro com tempo maior que o carro que deseja entrar então não é possível utilizar o estacionamento. Remova todos os carros do estacionamento (pilha) que tenha o tempo de saída menor ou igual ao tempo de chegada do carro atual. Depois basta inserir o carro no estacionamento. Outro ponto, se em algum momento, após remover os carros e um outro chegar, o estacionamento ficar com uma quantidade de carros igual ou superior a k então não é possível utilizar o estacionamento. Se no final foi possível colocar todos os carros no estacionamento então é possível utiliza-lo.
Um exemplo de implementação segue abaixo:
E - Teclado Quebrado
Resolva este problema: URI
A solução deste problema torna-se muito elegante e simples quando olhamos para a sequência digitada como uma lista de caracteres. Sendo assim, utilizaremos uma list de char e um iterator para o final da mesma (vamos chamar de it para efeito de explicação). Desta forma, quando o usuário digitar ’[’ faça it = lista.begin(), caso digite ’]’ faça it = lista.end(). Se uma letra for digitada insira a mesma na lista na posição onde o iterator está “apontando”, ou seja, lista.insert(it, caractere_digitado). No final basta imprimir a lista com os caracteres, simples e eficiente =).
Um exemplo de implementação segue abaixo:
F - Problema Fácil de Rujia Liu?
Resolva este problema: URI
São dados um vetor de n números inteiros e m consultas. Cada consulta consiste em perguntar: qual o índice (1-indexado) da k-ésima aparição do valor v no vetor dado? Podemos utilizar um map com o valor v como chave e um vector com as posições em que o valor v aparece. Mas como os valores vão ser no máximo 1.000.000, podemos utilizar um array no lugar do map, já que conseguimos alocar 1.000.000 posições em um array tranquilamente. Sabendo disso, basta a cada entrada de um número inserir a posição indexada de 1 no vector que está na posição v do nosso array, sendo v o valor do número inserido. Para responder consultas, é preciso verificar se o vector com as posições de um valor v tem tamanho menor que o k requerido, o que indica que não existe a k-ésima aparição. Nesse caso, imprimos 0 em uma linha. Caso contrário, basta imprimir a posição k-1 do vector, já que k começa em 1 e os índices de um vector começam de 0.
Um exemplo de implementação segue abaixo:
G - Ida à Feira
Resolva este problema: URI
Este problema também pode ser resolvido com uma busca linear no vetor com os preços para cada item que deseja comprar. No entanto, uma forma mais eficiente é armazenar os itens, juntamente com os preços, em uma estrutura de dados map < string, double > . Ou seja, para cada nome (chave) de um item associamos ao seu custo (valor). Basta percorrer a lista de compras e ir computando o custo total da compra.
Um exemplo de implementação segue abaixo:
H - Gerente de Espaço
Resolva este problema: URI
O problema em si não é difícil, mas sim trabalhoso (recomendo resolver primeiramente o problema Estacionamento, pois as operações presentes lá são semelhantes com as operações presentes aqui). O problema consiste em simular três operações em um disco com tamanho D (Kb, Mb ou Gb). A primeira operação insere um arquivo com identificador NOME . Aqui vale ressaltar o fato de como esse arquivo deve ser inserido: Um arquivo é sempre armazenado em um bloco de células de armazenamento contíguas. O arquivo a ser inserido deve ser sempre colocado no início do menor bloco livre cujo tamanho é maior ou igual ao tamanho do arquivo. Se mais de um bloco livre é igualmente adequado, escolha o mais próximo do começo do disco. Portanto, o arquivo não deve ser inserido no primeiro bloco livre que caiba o mesmo, mas sim, dentre todos os blocos que o comporte, no que tenha o menor tamanho e caso exista mais de um bloco com tal tamanho devemos escolher o que está mais perto do começo do disco. Já a segunda operação remove um arquivo com identificador NOME. Por fim, a terceira operação otimiza o disco, realocando os arquivos para o inicio do disco mas mantendo a ordem dos mesmos.
Observado as operações disponíveis, a primeira sugestão é trabalhar com o tamanho do disco em Kb, pois desta forma facilitará a manipulação dos blocos e da impressão da descrição do disco após as operações. As seguintes estruturas foram utilizadas:
Para representar o disco pode-se utilizar a estrutura de dados list composta por outra estrutura bloco. Esta última é composta pelas variáveis: tam que representa o tamanho do bloco; tipo que armazena o tipo do bloco (LIVRE ou OCUPADO); e nome que mantem salvo o nome do arquivo que está armazenado no bloco em questão. A estrutura de dados map, representado por arquivos, é utilizada com o intuito de acelerar a segunda operação (remoção), uma vez que a mesma mantem um “ponteiro” para o bloco cujo o arquivo está armazenado, por conseguinte a remoção torna-se direta, já que não há a necessidade de percorrer todo o hd procurando o arquivo a ser removido.
Antes de explicar em mais detalhes a solução vamos simular as três operações através de um caso de teste. Assim ficará mais simples de entender a solução empregada. Tal caso de teste é apresentado a seguir:
O primeiro passo é converter a unidade do disco de 8Mb para 8192Kb. No inicio o hd tem um único bloco livre com o tamanho da sua capacidade:

A primeira operação é do tipo insere. Deseja-se inserir o arquivo arq0001 de tamanho 4096Kb (4Mb). Tal operação é possível uma vez que o hd tem um bloco livre de tamanho 8192Kb.
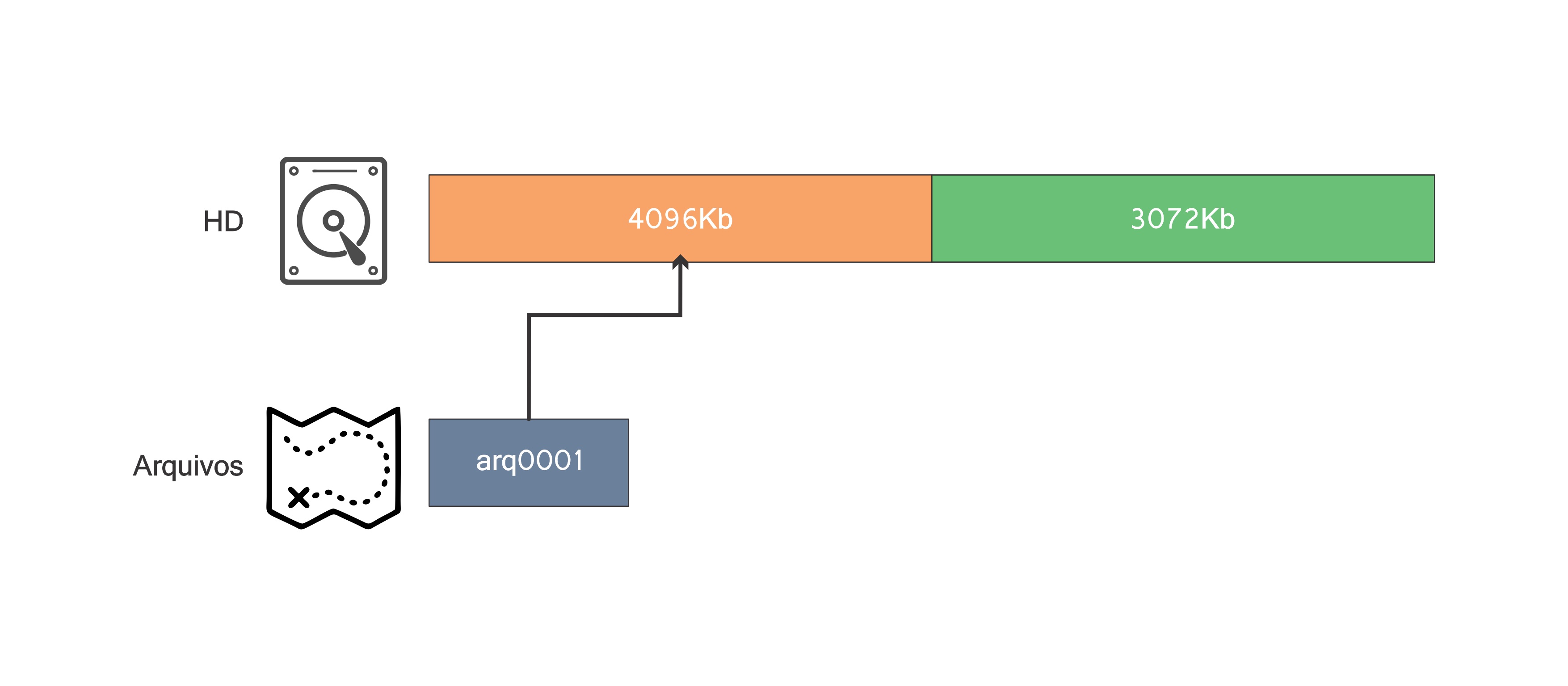
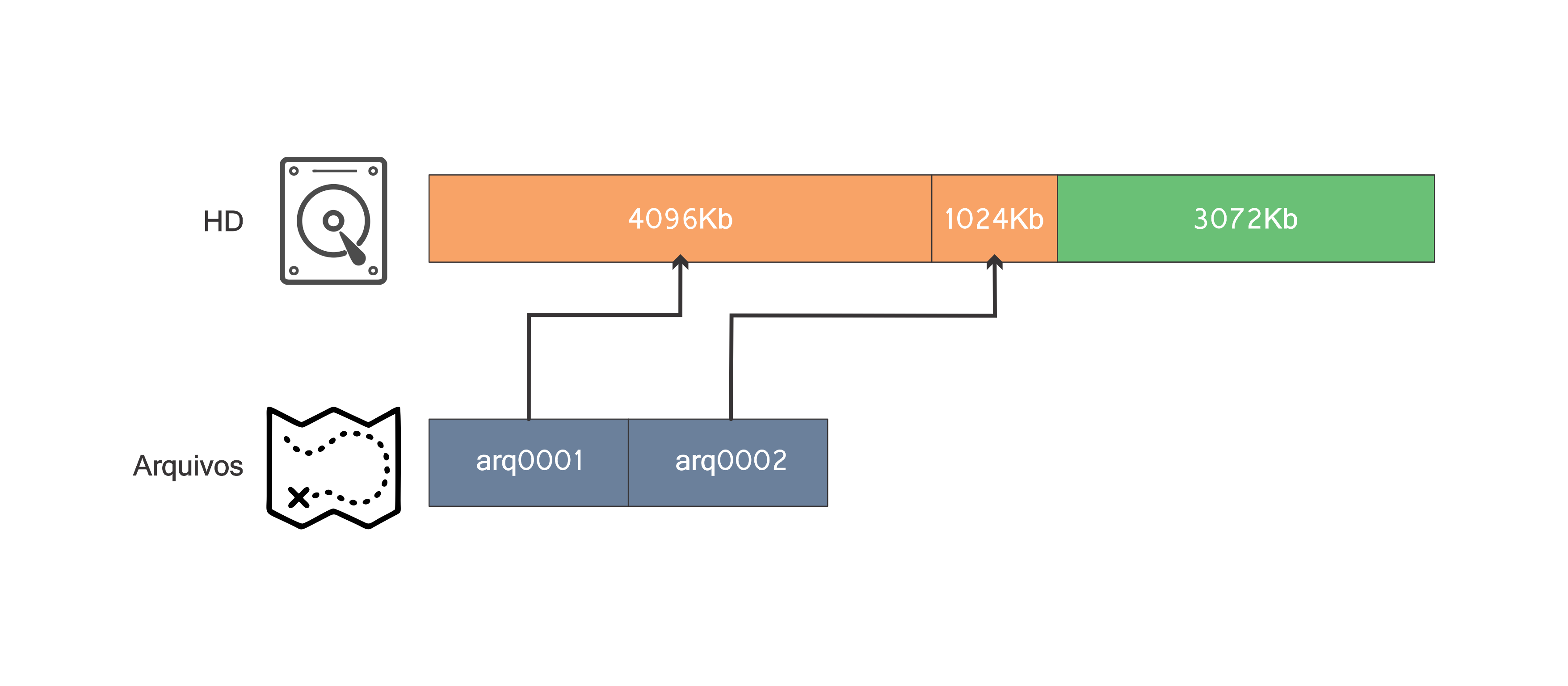
O hd agora tem dois blocos, ambos de tamanho 4096Kb, mas o primeiro contendo o arquivo arq0001 e o segundo livre. Observe que agora o mapa arquivos tem um “ponteiro” do arquivo arq0001 para o bloco no qual foi alocado. De forma análoga, a próxima operação é realizada:
A seguinte também:
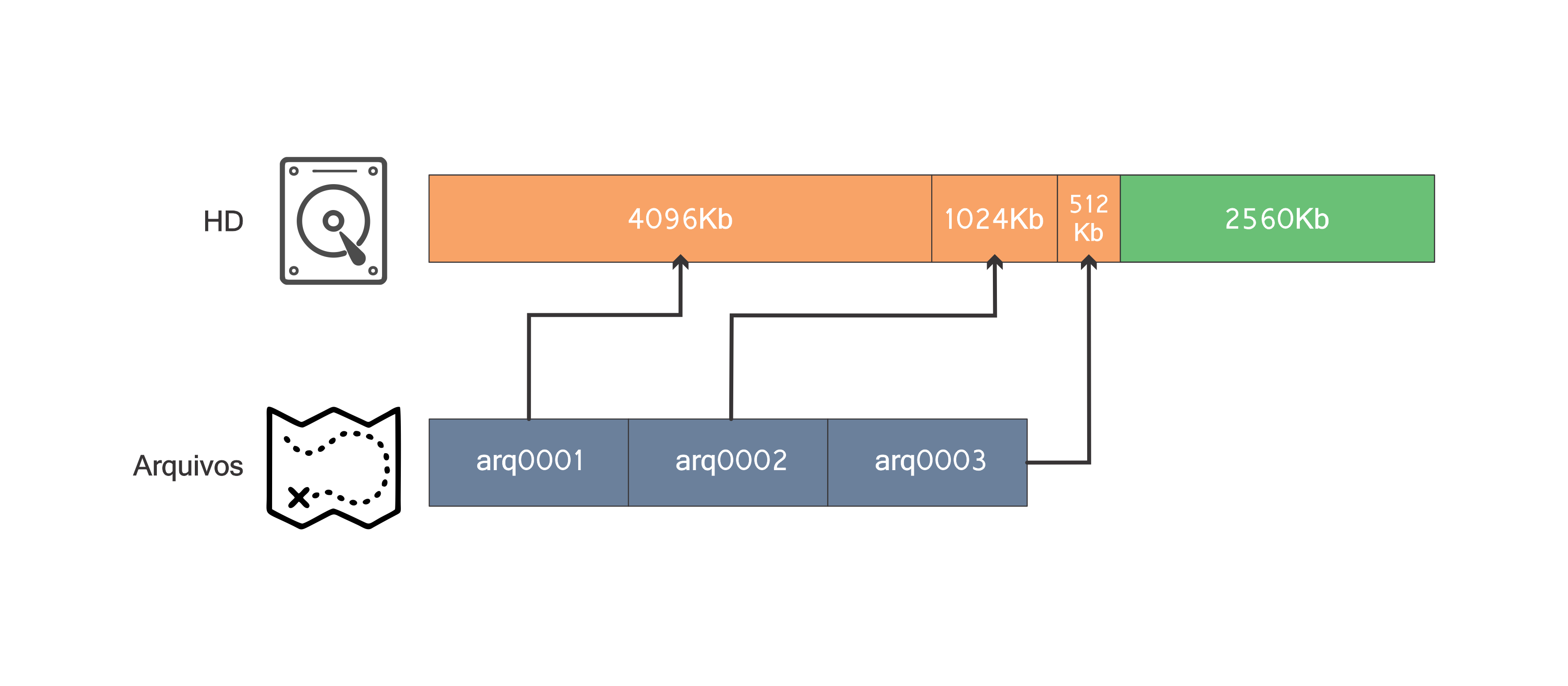
A próxima operação é de remoção, tal operação pode ser realizada diretamente, uma vez que já é sabido o bloco cujo o arquivo arq0001 está alocado. Agora um novo bloco com tamanho 4096Kb está livre (a próxima operação é ignorada já que o arquivo não está alocado no hd):
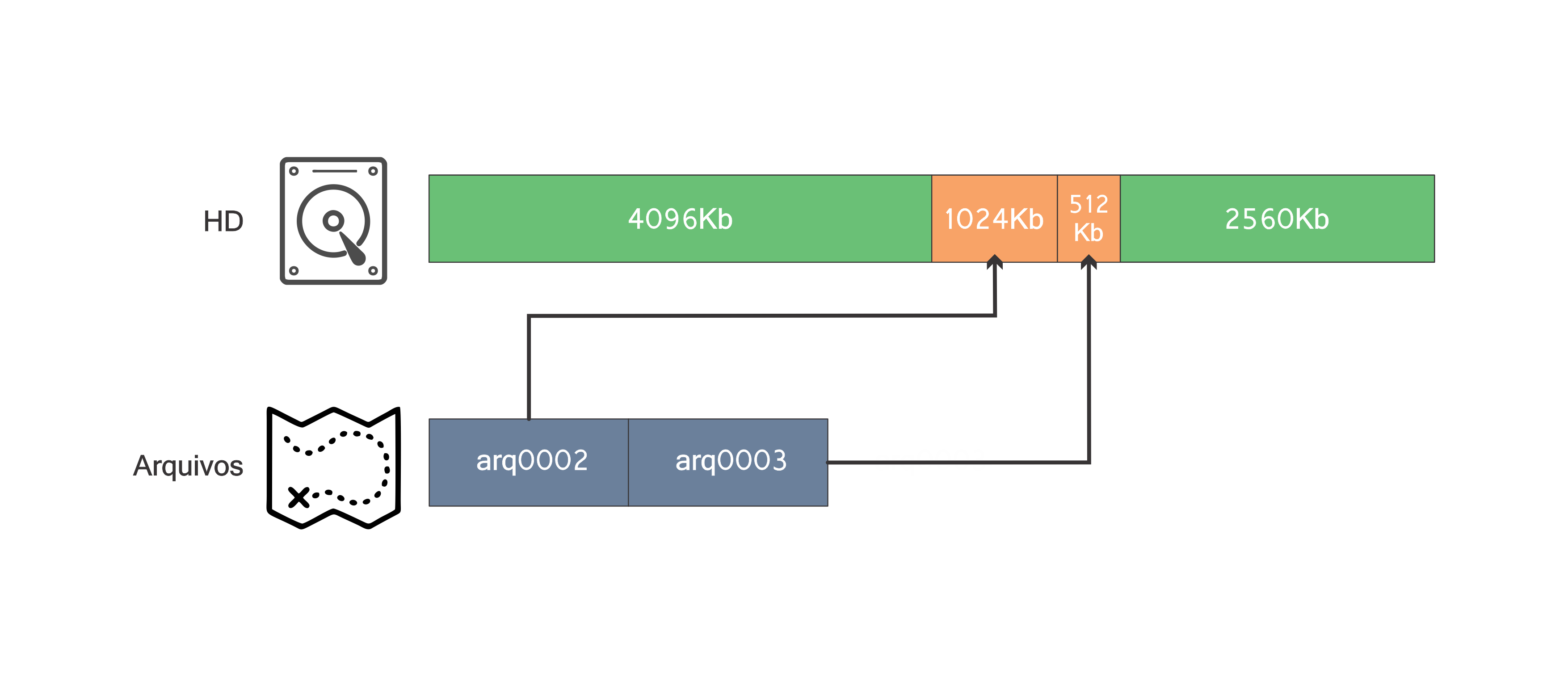
A próxima operação válida é de inserção, mas não há espaço em disco para o arquivo arq0001. Seguindo as instruções do enunciado do problema, uma operação de otimização deve ser realizada. O hd então ficará dessa forma:
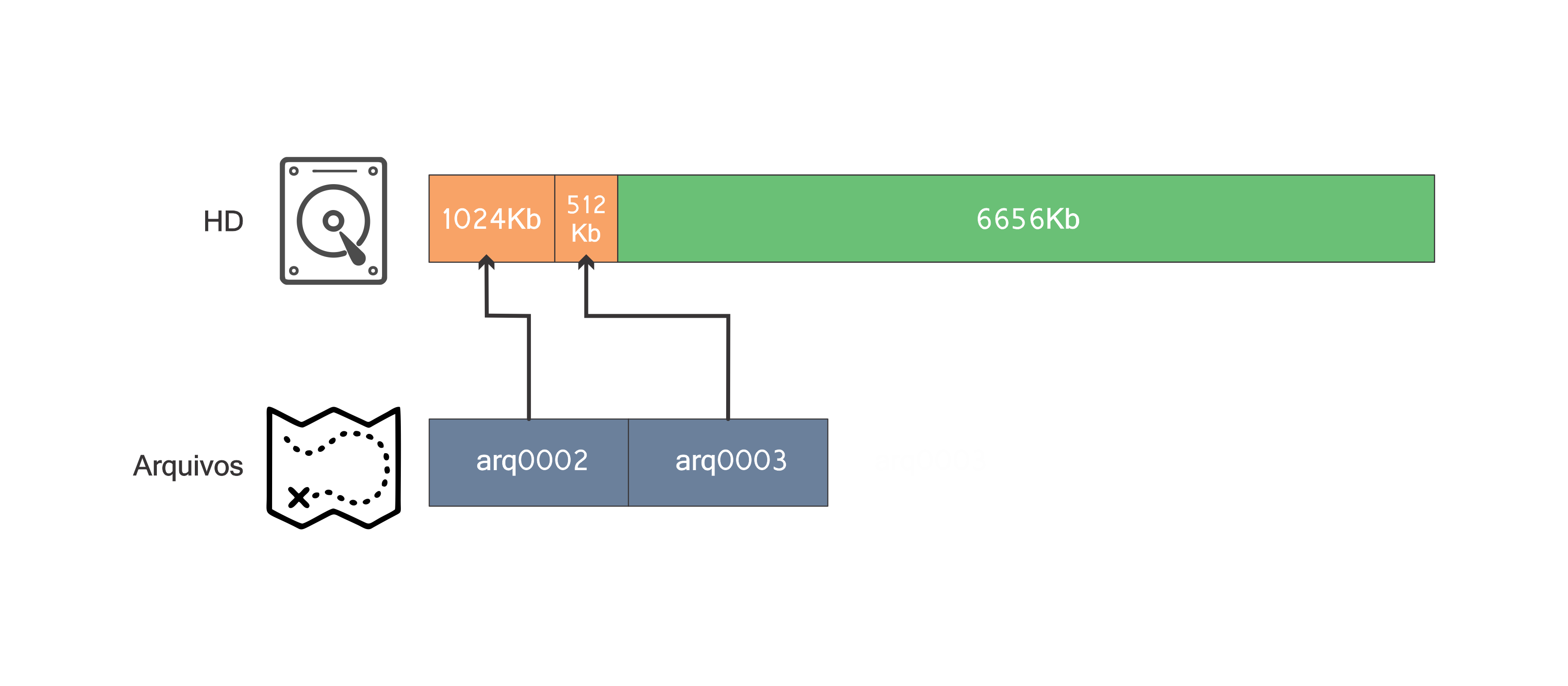
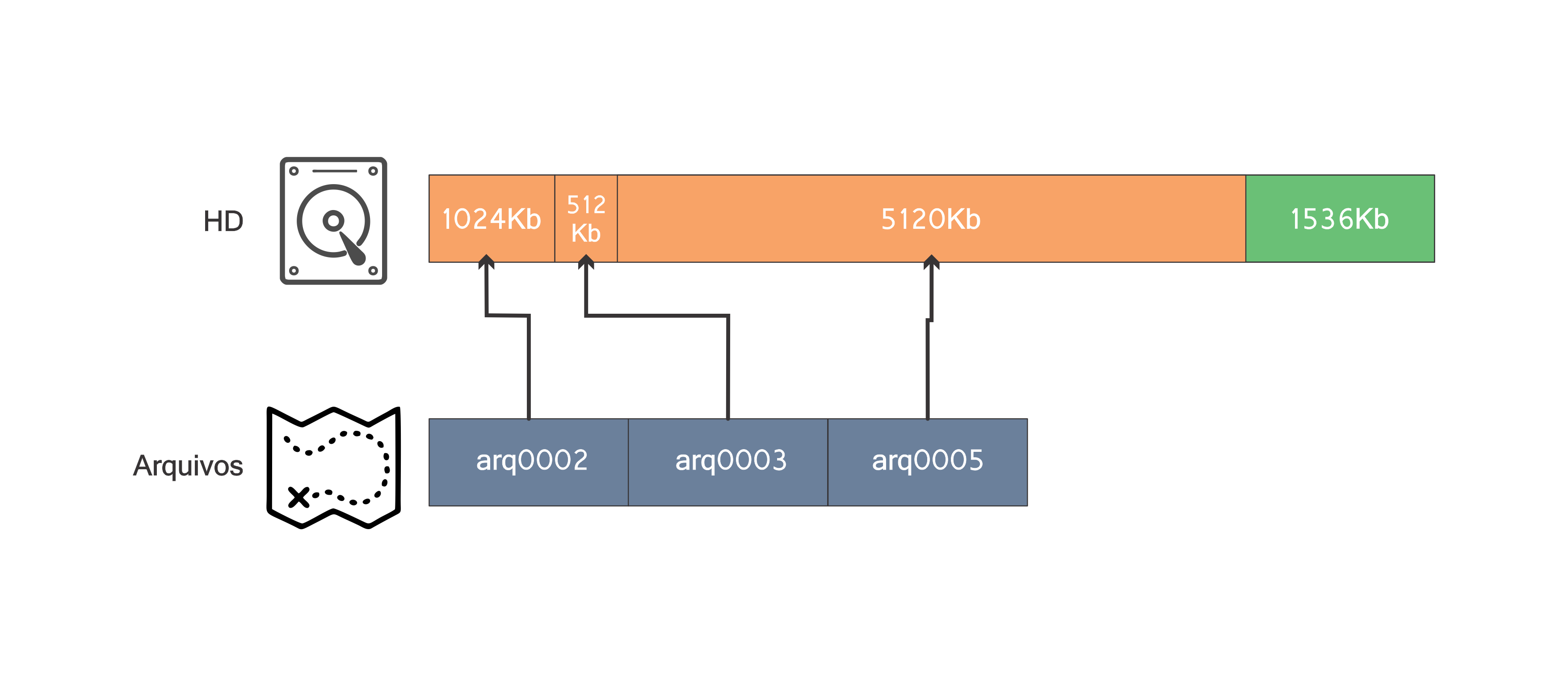
Note a mágica dos “ponteiros” ocorrendo =). Com um bloco livre de tamanho 6656Kb o arquivo arq0001 com tamanho 5120Kb pode ser inserido:
Portanto, a ideia é simular o hd como uma lista de blocos. Cada um destes blocos têm um tamanho em Kb e podem ser do tipo LIVRE ou OCUPADO. A seguir será mostrado como implementar as três operações no hd:
InserçãoA ideia aqui é percorrer todo o hd procurando os blocos que tenham o tamanho maior ou igual ao tamanho do arquivo que se deseja inserir. Note que a função insere encontra a posição cujo o bloco comporta tal arquivo e seja o menor possível dentre os que satisfaz a condição. Definido o bloco, basta inserir o arquivo no mesmo, caso o bloco seja maior que o arquivo então um pedaço do bloco ainda estará disponível, assim basta inserir o bloco livre restante no hd para que possa ser utilizado por outro arquivo.
RemoçãoO primeiro passo é verificar se o arquivo está no hd (linha 2). Caso não esteja não há nada a ser feito. Por outro lado, se estiver deve-se remove-lo. Lembre que o map arquivos mantem o “ponteiro” para o bloco que tem o arquivo em si armazenado, basta remove-lo da lista e dos arquivos. Existem três situações podem ocorrer antes da remoção. Os mesmo são ilustrados a seguir:
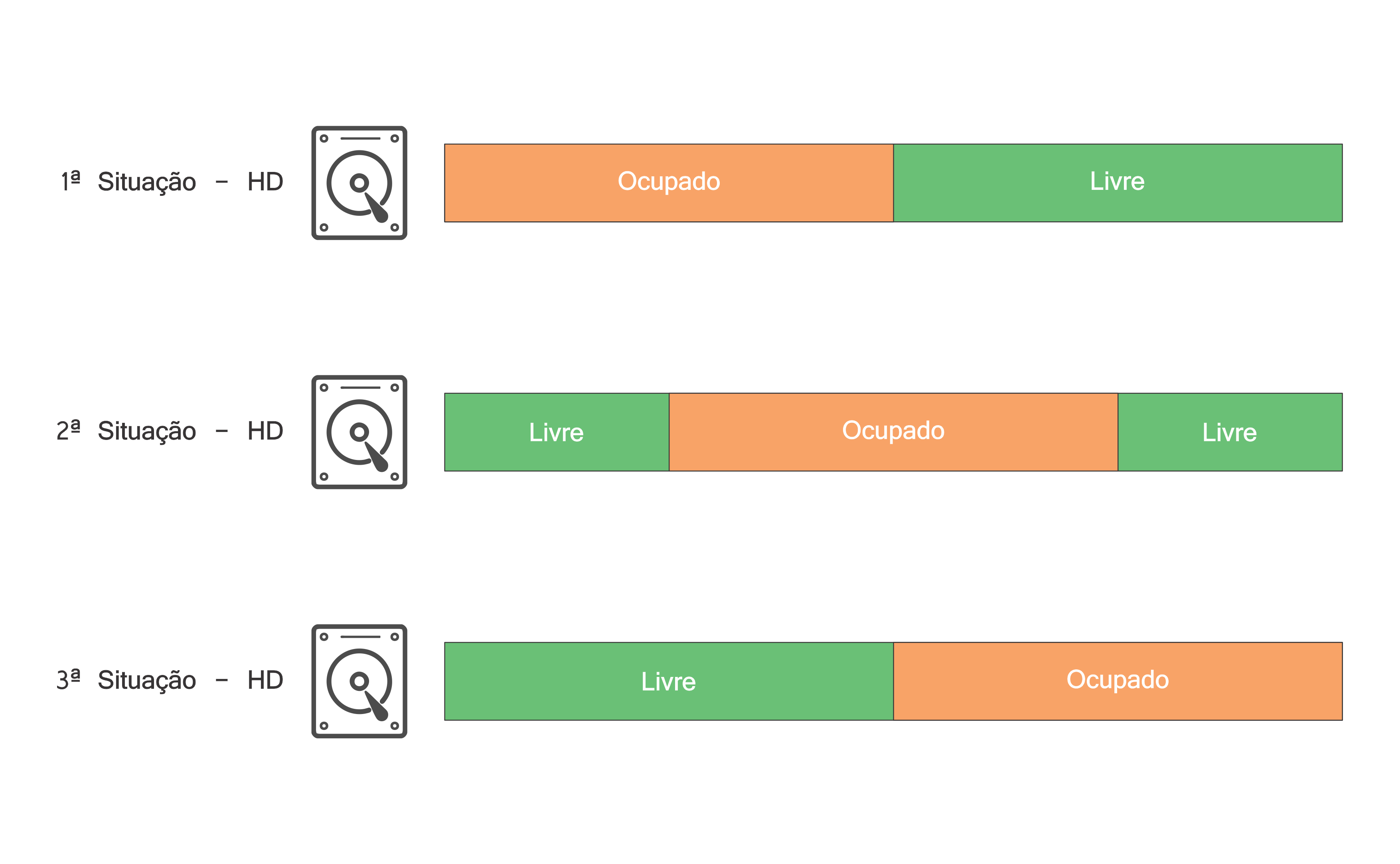
Na primeira situação o arquivo que será removido está do lado esquerdo de um bloco livre. Neste caso após a remoção deve-se realizar o merge dos blocos, gerando assim um único bloco com o valor do tamanho obtido pela soma dos valores do tamanho do bloco que continha o arquivo com o tamanho do bloco livre. Na segunda situação o arquivo que será removido está entre dois blocos livres. De forma parecida com a primeira situação, será realizado o merge do bloco que tinha o arquivo com os blocos da direita e da esquerda. Na terceira situação o procedimento é análogo a primeira situação, mas no caso o merge é realizado com o bloco da esquerda. Estas operações de merge são mostrada a seguir:
OtimizaçãoPara realizar a operação de otimização basta percorrer todo o hd e ir contabilizando/removendo os blocos livre. No final, caso o valor contabilizado seja diferente de zero, basta criar um novo bloco com o valor do tamanho igual ao contabilizado. Segue um exemplo de implementação de tal operação:
Após todas as operações terem sido realizadas, a útltima etapa consiste em percorrer o hd e computar a porcentagem de espaço livre em cada segmento de tamanho igual a capaidade do hd dividido por 8 – vamos armazenar este valor de tamanho em uma variável chamada limite. Note que os blocos do hd em si podem ter tamanhos maiores ou menores que o limite. Cada bloco é do tipo LIVRE ou OCUPADO – vamos criar outras duas variáveis: livre e ocupado. Elas irão manter o acumulado dos tamanhos dos blocos do tipo LIVRE e OCUPADO, respectivamente. Então ao percorrer os blocos do hd, partindo do inicio para o final, se livre + ocupado ≥ limite então um bloco de tamanho limite foi preenchido e devemos imprimir a porcentagem de espaço livre do mesmo. O bloco atual observado fez ultrapassar o limite, se o mesmo for do tipo LIVRE então a variável ocupado deve ser zerada, por outro lado, se for do tipo OCUPADO então a variável livre é que deve ser zerada. Wat? Note que se o valor limite foi atingindo ou ultrapassado, então um novo bloco de tamanho limite deve ser “preenchido”. Se o bloco atual é do tipo LVIRE então o acumulado em ocupado não irá afetar o novo bloco, da mesma que o acumulado em livre não afetará se o tipo do bloco for OCUPADO.
A implementação completa segue abaixo:
I - Espécies de Madeira
Resolva este problema: URI
Uma das forma de resolver este problema de maneira eficiente é utilizando a estrutura de dados map < string, double > . A chave será o nome da espécie e o valor a quantidade de árvores de tal espécies. Assim, a solução consiste em percorrer as espécies (que já estarão ordenadas) e imprimir a porcentagem de árvores que ela representa.
Um exemplo de implementação segue abaixo:
J - Pontos de Feno
Resolva este problema: URI
Uma das forma de resolver este problema de maneira eficiente é utilizando a estrutura de dados map < string, int > para o dicionário. A chave será a palavra e o valor o total, em dólar, associado a tal palavra. Assim, a solução consiste em percorrer as palavras informadas e adicionar o seu valor, caso a palavra lida esteja no dicionário, ao salário do funcionário.
Um exemplo de implementação segue abaixo:
K - Eu Posso Adivinhar a Estrutura de Dados!
Resolva este problema: URI
Excelente problema! Permite utilizar três estruturas de dados: stack de frango, queue e priority_queue. A ideia é simular, ao “mesmo tempo”, as três estruturas. Sem em algum momento a entrada ferir uma das estruturas então tal estrutura será descartada como possibilidade. No final se a quantidade de estruturas descartas for inferior a duas então não é possível saber qual estrutura de dados foi utilizada. Caso todas tenham sido descartadas então não pode ser nenhuma das estruturas =P. Por fim, se sobrar apenas uma então está é a estrutura que reflete o comportamento dos dados fornecidos.
Um exemplo de implementação segue abaixo:
L - Jogando Cartas Fora
Resolva este problema: URI
O comportamento descrito no enunciado reflete as operações de uma fila. Portanto, basta utilizar a estrutura de dados queue para simular as operações descritas.
Um exemplo de implementação segue abaixo:
N - Estacionamento
Resolva este problema: URI
Uma da formas de resolver este problema é através da simulação do estacionamento pela estrutura map < int, int >. A ideia é simular os espaços livres do estacionamento, desta forma a chave do map é composta pelo inicio do segmento de espaço livre e o valor o final de tal segmento. Podemos manter também um vetor de pair < int, int >, onde cada posição representa uma placa de um carro e o pair armazena o inicio e o fim do segmento de espaço do estacionamento onde o carro está estacionado. Desta forma não precisamos percorrer todo o estacionamento procurando o carro que será removido. Para efeito de entendimento vamos simular o segundo caso de teste do enunciado:
Tamanho do estacionamento igual a 30
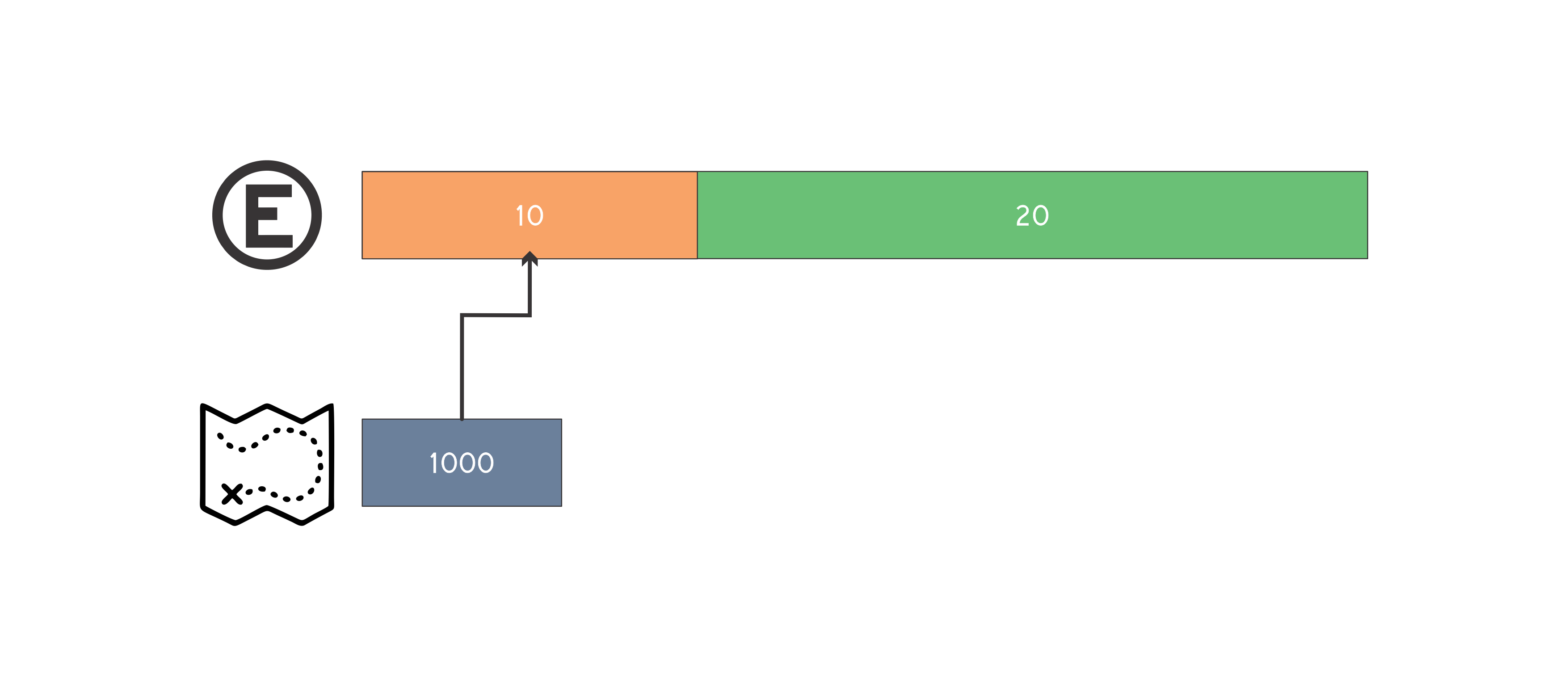
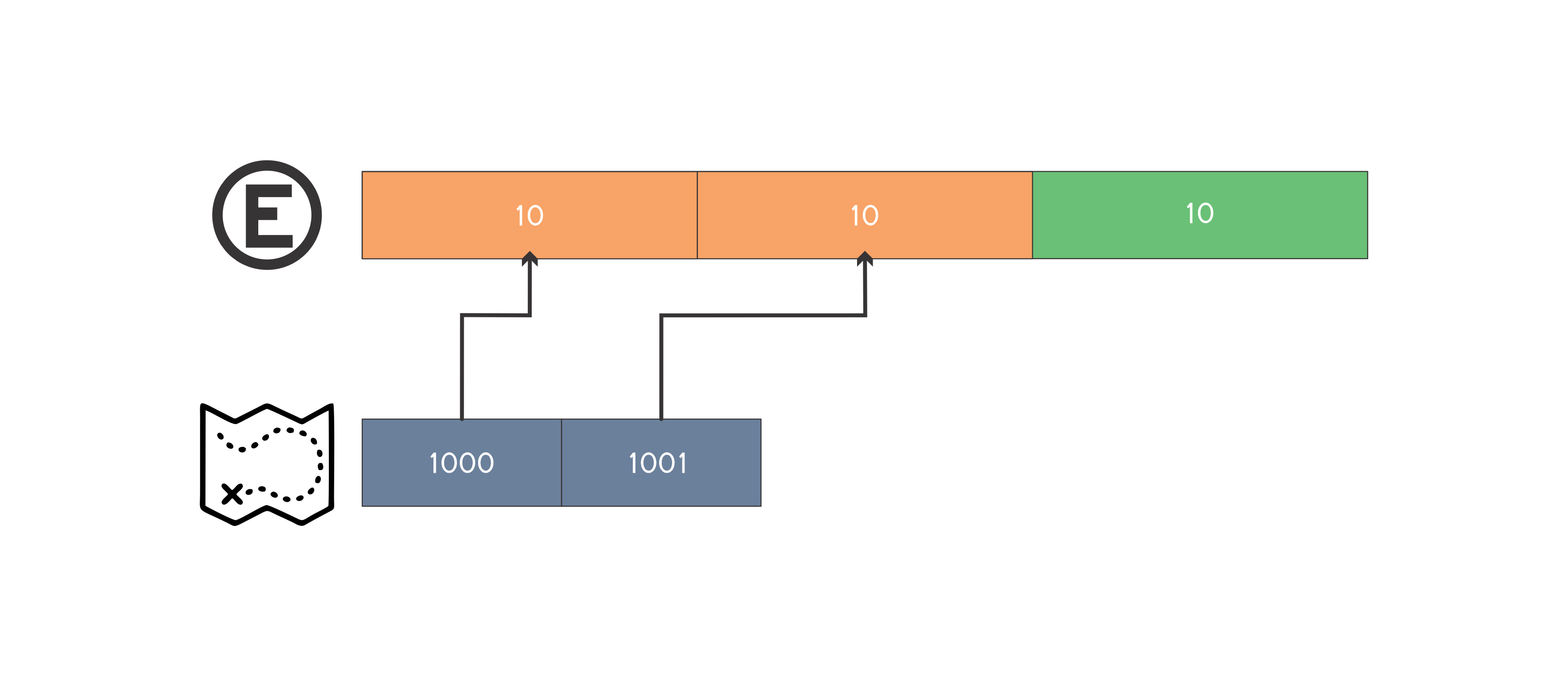
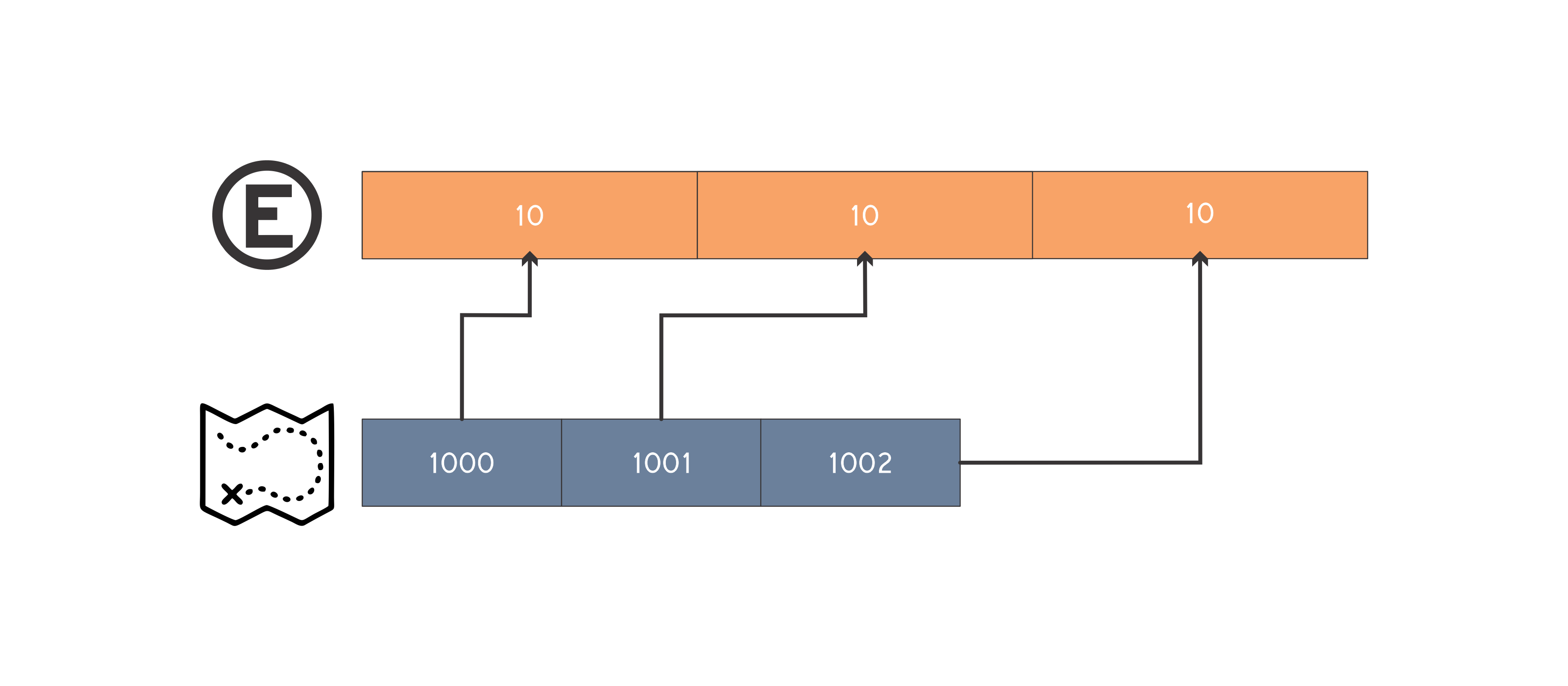
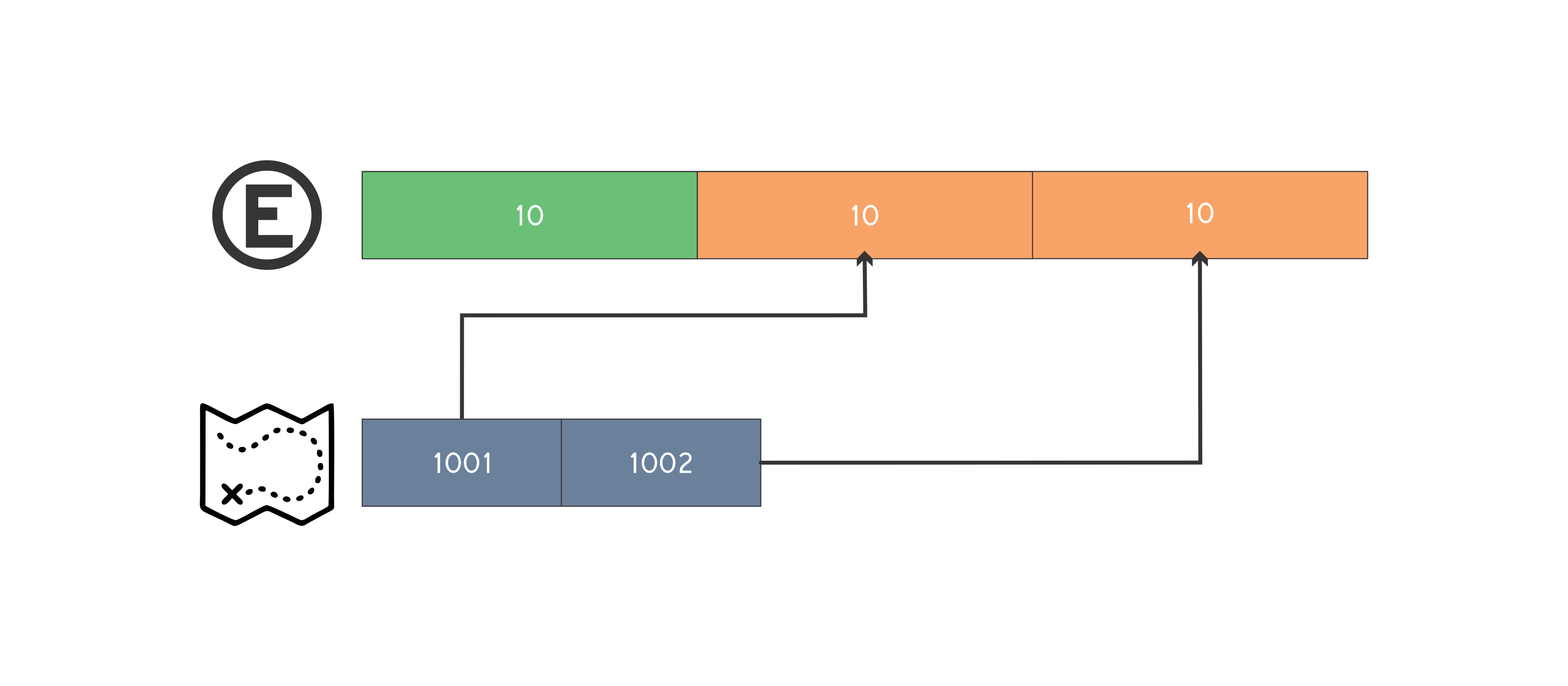
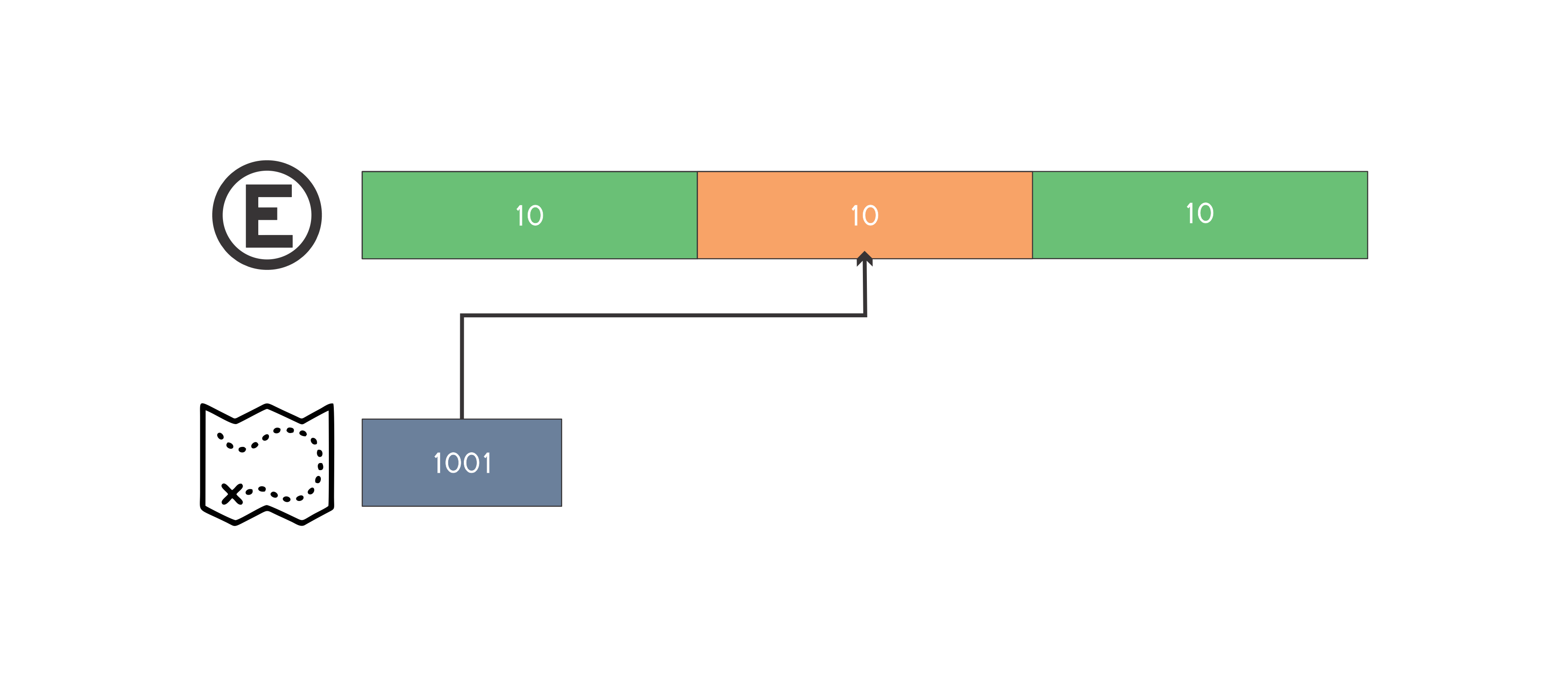

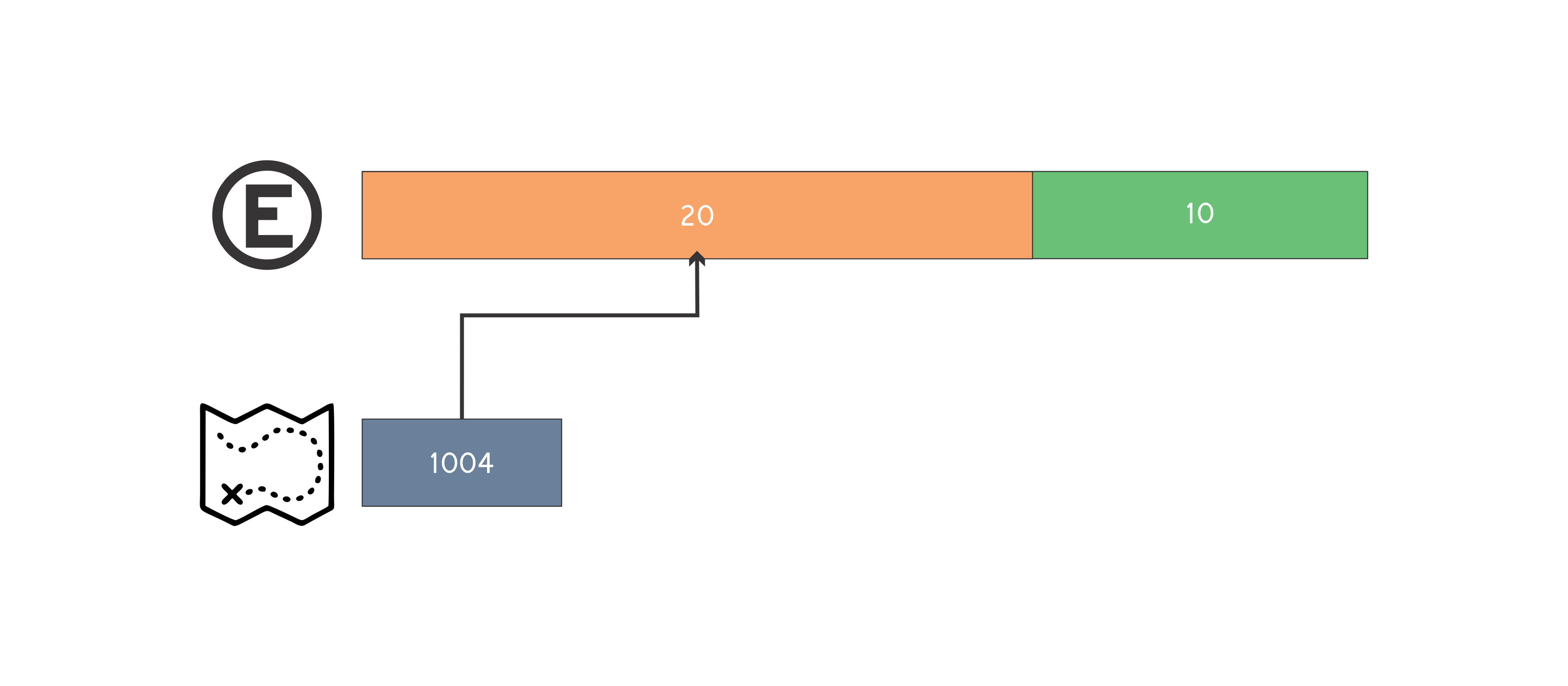

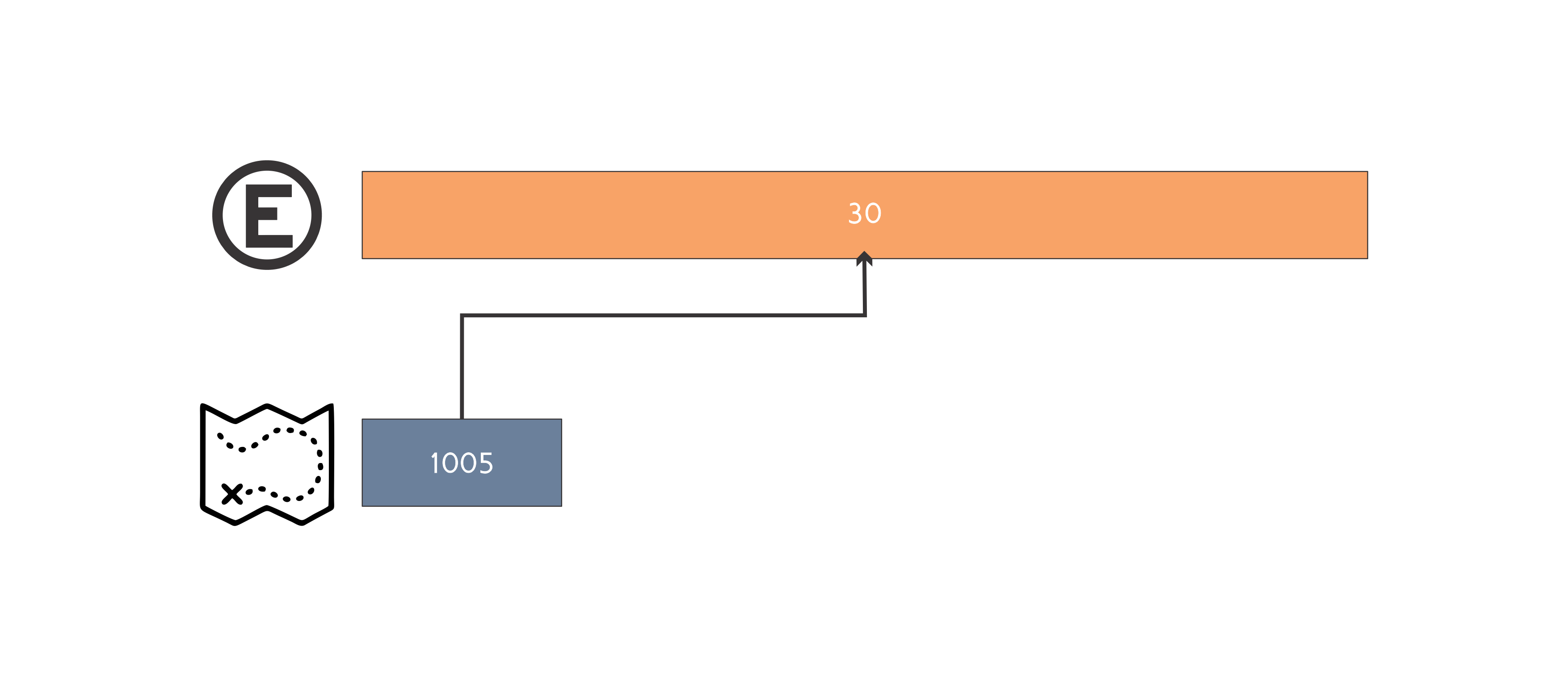
Um exemplo de implementação segue abaixo: