Este post tem como objetivo apresentar algumas técnicas e dicas que irão auxiliar na resolução dos problemas do BOCA.
Problemas discutidos:
| Problema | Dificuldade | Técnica relacionada |
|---|---|---|
| Imperador Kaktus |   |
BFS |
| Recruta militar |   |
Floyd-Warshall |
| Entregador de pizza |  |
BFS |
| Oxigenio |   |
BFS |
| Labirintos |   |
BFS |
| Robo colecionador |  |
Ad hoc |
| A jornada do rato |  |
Ad hoc |
| Caminhada na montanha |   |
BFS |
| Perseguicao do cavalo |    |
BFS de estado |
A1 - Imperador Kaktus

Alguns pontos importantes que devemos observar no problema são:
- A cada minuto a inundação se expande para todos os campos vazios que têm pelo menos um lado em comum com um campo alagado.
- O Pintor e os três pequenos Ouriços não podem passar através das rochas e nem por campos inundados.
- A toca do Castor nunca será inundada. (Note que a água não irá expandir através da toca do Castor).
- O Pintor e os três pequenos Ouriços deslocam-se simultaneamente com a inundação. Mas o Pintor e os três pequenos Ouriços não podem se mover para um campo que está prestes a ser inundado no mesmo instante (minuto).
Levantados tais pontos, o problema pede para computar o menor tempo necessário para o Pintor e os três pequenos Ouriços alcançarem com segurança a toca do Castor. Podemos utilizar um único BFS para resolver tal problema. No entanto, acho mais intuitivo rodar dois BFS’s, um para descobrir o instante que cada campo será inundado e outro para descobrir o menor tempo necessário para o Pintor e Cia chegarem na toca do Castor.
Um exemplo de execução dos BFS é mostrado na Figura abaixo. O caso de teste utilizado é o terceiro do enunciado do problema. Note que no lado esquerdo da Figura temos o preenchimento da matriz de tempos de inundação executado pelo BFS (Inundação). No lado direito é apresentado a execução do BFS (Pintor e Cia), onde o Pintor e Cia só irá mover para um campo caso o mesmo tenha sido inundado em um instante posterior ao tempo que o Pintor e Cia acabara de chegar. Os campos em vermelho são os que não podem ser alcançados e os verdes o que podem. Os números com cor azul representam os tempos de inundação dos campos e os com cor laranja os tempos que Pintor e Cia chegaram nos campos.
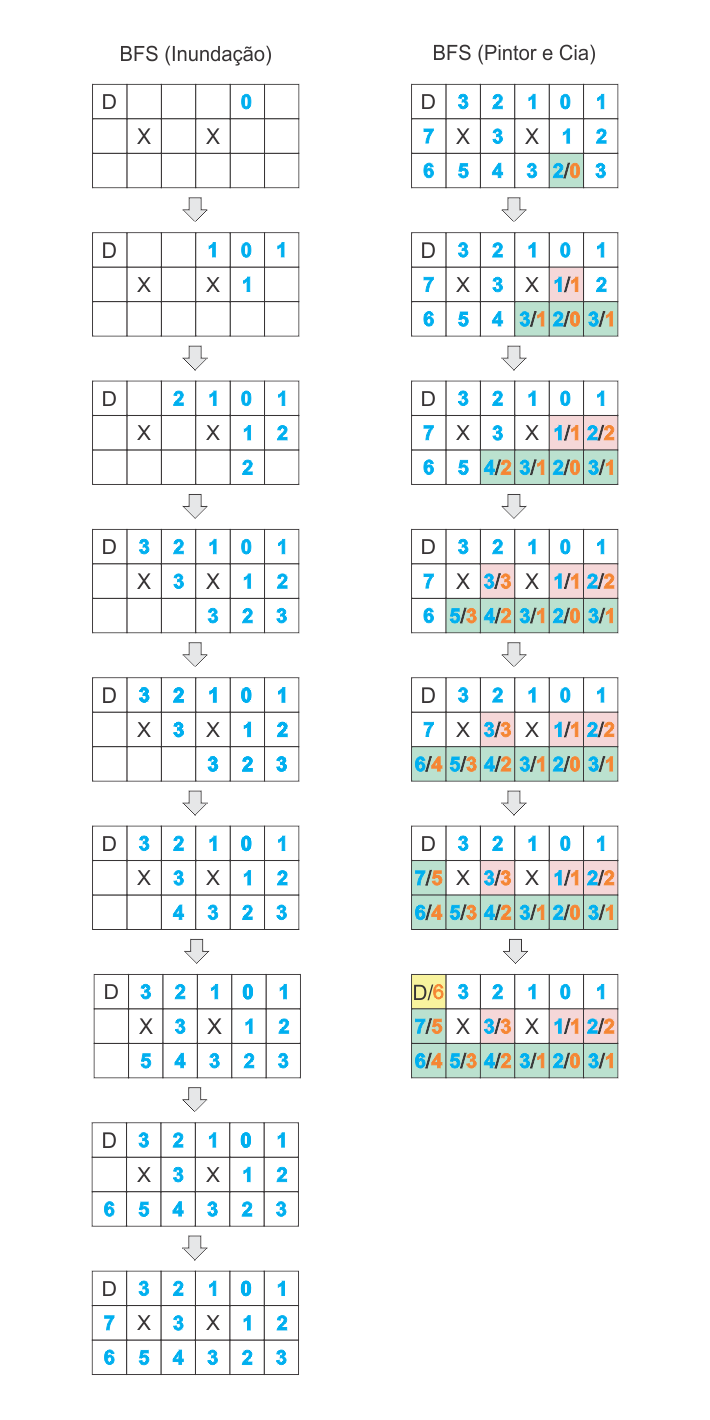
Um exemplo de implementação segue abaixo:
Uma outra abordagem, desenvolvido por Rafael Leão Ramos, utilizando um único BFS apresenta a seguinte ideia: "Cada ciclo do BFS equivale à um minuto na floresta encantada, a cada ciclo a água e o Pintor e cia se expandem, a água deve se expandir primeiro porque o Pintor e cia não podem se mover para um campo que será inundado no mesmo minuto.
Só será usada uma matriz para armazenar os caracteres, também será a partir dela que os elementos irão se expandir e ela também servirá como matriz de visitados.
No começo de cada ciclo ans é incrementado, ans armazena o tamanho de minutos gastos.
A cada ciclo é verificado o tamanho de cada fila, e então um "for" percorre a fila de 0 até esse tamanho removendo os elementos do "front" e ignora os elementos que estão sendo adicionados nesse loop, eles só serão verificados no próximo ciclo.
Se o Pintor e cia(S) conseguirem se expandir até a toca do castor(D) é impresso na tela o total de minutos gastos, e programa encerra. Caso o BFS termine sem S se expandir até D a palavra "KAKTUS\n" é impressa;"
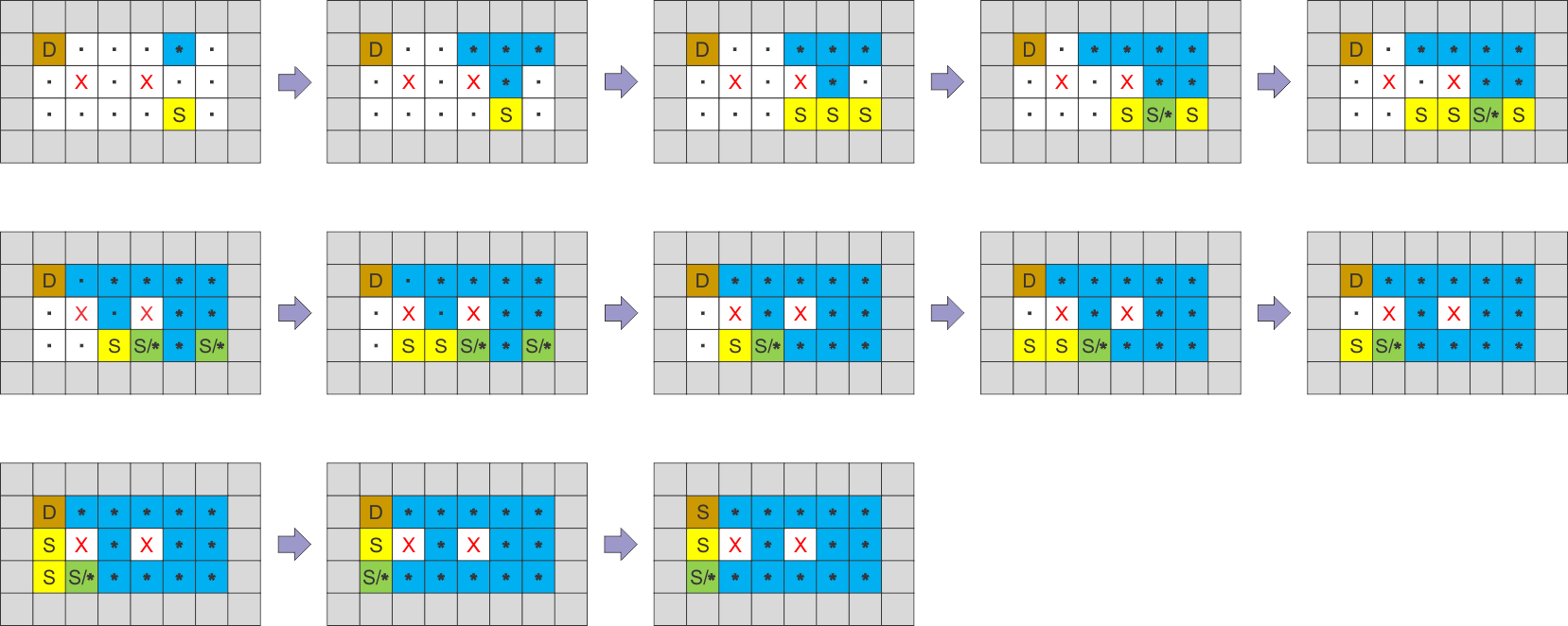
Um exemplo de implementação segue abaixo:
B1 - Recruta militar
O problema pede para que, dado um conjunto de locais e as possíveis conexões entre tais locais, ajude João a encontrar o Kth menor distância entre esses pares de locais de forma que tal escolha ocorra com probabilidade mínima p.
O primeiro ponto que deve-se observar é que será necessário computar as distâncias mínimas entre todos os pares de locais. Para essa tarefa pode-se utilizar o algoritmo de Floyd-Warshall, uma vez que o número de locais é 100 e as distâncias entre as possíveis conexões e dado como uma matriz de adjacência. O segundo ponto é que será necessário ordenar as distâncias mínimas calculadas, já que será necessário encontrar a Kth delas.
Seja S o conjunto de distâncias mínimas entre todos os pares, segundo o enunciado a probabilidade de escolher uma dessas distâncias é igualmente provável, ou seja, 1/S.Desta forma, a probabilidade de qualquer distância mínima entre a primeira e a Kth será Kth/S. Deseja-se que Kth/S seja pelo menos p, portanto, Kth/S ≥ p, simplificando, Kth ≥ p * S. Como é pedido a menor dentre as distâncias mínimas possíveis, então chega-se que a resposta será a distância mínima que esteja na posição Kth = ⌈p * S⌉-1, o teto é para definir uma posição inteira, ou seja, se cair na posição 4,02 na verdade será a posição 5. O -1 é necessário porque o vetor que armazena as distâncias mínimas é indexado de 0.
Um exemplo de implementação segue abaixo:
C1 - Entregador de pizza
O enunciado do problema fornece a modelagem utilizada para indicar as possibilidades de movimento a partir de uma localização do entregador de pizza. Dado tal modelagem, o problema consiste em determinar a quantidade mínima de intersecções que o entregador de pizza passa ao se mover da extremidade mais Noroeste (1,1) da cidade para a extremidade mais a Sudeste (l,c) da cidade.
Este problema pode ser resolvido com um BFS, uma vez que a quantidade de interseções entre duas localizações adjacentes é 1.
Um exemplo de implementação segue abaixo:
D1 - Oxigênio
Este problema exige uma boa interpretação do enunciado. Destaca-se então alguns trechos do enunciado:
- Ele está numa altitude em que não precisa usar o balão de oxigênio reserva, mas ao se mover para qualquer posição mais elevada o uso do oxigênio será necessário. Neste ponto que pode ocorrer uma interpretação erronia do problema, uma vez que o enunciado não deixa muito claro se será necessário o uso do oxigênio quando estiver em uma posição mais alta que a anterior ou, caso esteja em qualquer posição, será necessário o uso do oxigênio se tal posição for mais alta que a primeira posição (1,1). A segunda interpretação é a correta.
- [...]não pode subir ou descer mais de 2 unidades de altitude em um único passo. Já aqui é em relação a posição atual do alpinista, ou seja, se o mesmo está na posição (i,j) e deseja ir para a posição (i+1,j), só será possível desde que a diferença de altitude entre alas seja menor ou igual a 2.
- Se a altitude do ponto inicial (final) requer oxigênio, uma unidade de oxigênio é consumida pelo alpinista durante o passo para sair dessa (chegar nessa) posição. Suponha, novamente, que o alpinista esteja na posição (i,j) e deseja deslocar-se para a posição (i+1,j), sejam H1, H2 e H3 as altitudes das posições (1,1), (i,j) e (i+1,j), respectivamente.
Ciente de tais trechos, o problema então consiste em encontrar o caminho entre as posições (1,1) e (n,n) que exija menor consumo de unidades de oxigênio. Tal problema pode ser resolvido com um BFS.
Um exemplo de implementação segue abaixo:
E1 - Labirintos
Como os demais problemas discutidos anteriormente, este problema pode ser resolvido com BFS. O único ponto que deve-se observar, já que não é deixado claro no enunciado, são os movimentos possível que o competidor pode realizar. No caso, ele pode mover-se para as quatro direções (Norte, Sul, Leste e Oeste), desde que tal direção não leve para uma posição que tenha o caractere *.
Um exemplo de implementação segue abaixo:
F1 - Robô colecionador
A solução deste problema não requer nenhuma técnica especifica. O enunciado descreve muito bem a modelagem e movimento do robô, de forma que só precisa implementar o que é descrito.
Um exemplo de implementação segue abaixo:
G1 - A jornada do rato
O rato pode mover-se para direita ou para baixo. O mesmo não pode ir para uma gaiola que tenha um gato. O enunciado pede para calcular a quantidade de caminhos que o rato pode fazer ao partir da posição (1,1) e chegar na posição (l,c). Olhando para os movimentos possíveis do rato, se ele está em uma posição (i,j), os movimentos possíveis são: ir para a posição (i+1,j) ou para a posição (i,j+1). Certo, vamos olhar para esses movimentos da perspectiva da posição que se deseja ir. Se o rato está na posição (i, j), ele pode ter vindo da posição (i-1,j) ou da posição (i, j-1). Desta forma, a quantidade caminhos possíveis para chegar na posição (i, j) vai ser a soma das quantidades de caminhos para chegar nas posições (i-1, j) e (i, j-1).
A Figura abaixo ilustra um exemplo dessa ideia. Note-se que o rato inicia na posição (1, 1) e deseja chegar na posição (3, 4). Com o intuito de eliminar alguns ifs na implementação, foi criado uma borda na parte esquerda e superior da matriz. A cada passo, podemos ir computando a quantidade de caminhos possíveis, repare na posição (3, 3), o total de caminhos é dado por 2, já que existe um único caminho para chegar nas posições (2, 3) e (3, 2). Por outro lado, na posição (3, 4) descobrimos que existem 3 caminhos possíveis.

Um exemplo de implementação segue abaixo:
H1 - Caminhada na montanha
O enunciado é bem claro e direto, dado um mapa de altura de uma cadeia de montanhas e a restrição de que um caminhante amador se mover para um local adjacente (esquerda / direita, para cima / para baixo, mas não diagonalmente) somente se a diferença de altura com a localização atual for no máximo 1, o problema consiste em determinar o menor número de etapas necessárias para cruzar a cadeia de montanhas entre as bordas esquerda e direita de uma determinada área quadrada. As etapas contadas são as transições de um local para o próximo. Oura informação importante é a de que um caminhante pode começar em qualquer uma das posições mais à esquerda.
Ciente das restrições e movimentos possíveis, este problema pode ser resolvido com BFS. Para cada linha i e coluna j = 1, realize um BFS partindo dessa posição e compute a menor distância para as posições na última coluna, ou seja, j = c.
Um exemplo de implementação segue abaixo:
I1 - Perseguição do cavalo
Dado a posição de um peão e de um cavalo em um tabuleiro de xadrez ( com dimensão variável), o enunciado pede para computar a menor quantidade de movimentos que o cavalo deve realizar para capturar o peão. Se tal evento não seja possível, então deve-se informar a menor quantidade de movimentos do cavalo que gere um empate ( peão em um posição (i, j) e o cavalo em uma posição (i+1, j)). Se mesmo assim não for possível ocorrer um empate então o peão ganha, uma vez que o mesmo irá conseguir chegar na última linha do tabuleiro. Deseja-se, também, nesse caso a menor quantidade de movimento do cavalo.
Esse problema pode ser resolvido com um BFS de estados. O estado nesse contexto nada mais do que a posição do cavalo, a posição do peão, a quantidade de movimentos realizados pelo cavalo e um valor que informa de quem é a vez de jogar (peão ou cavalo). Tal estado pode ser representado por uma Struct. Segue um exemplo.
A transição de um estado para o outro no BFS ocorre da seguinte forma:
- Se o turno é do peão então ele movido uma casa para frente, nesse momento deve-se verificar se o mesmo está na mesma posição do cavalo, se estiver então ocorreu empate, se esse foi o primeiro empate deve-se salvar a quantidade de movimento do cavalo. No caso de empate ou se o peão chegar na última linha do tabuleiro não há próximo estado para colocar na fila.
- Se o turno é do cavalo, então quando ele mover deve-se verificar se ele ganha, ou seja, se fica na mesma posição do peão, caso fique então o cavalo consegue ganhar, basta retornar a quantidade de movimentos que ele chegou nesse estado. Existem três repostas possíveis, vitória, empate ou derroa. Para ter controle de qual ocorreu, pode-se utilizar duas variáveis: win = -1 e empate = -1 que irá armazenar o primeiro momento que o cavalo vence e o primeiro momento que ocorreu um empate, respectivamente.
Desta forma, após o BFS, se a variável win estiver com -1 então o cavalo não ganhou, nesse caso deve-se verificar se a variável empate é diferente de -1, se for então ocorreu um empate. Caso contrário o cavalo perdeu com max(0,(L-peao.x)-1) movimentos, já que se ele não ganhou então quer dizer que o peão chegou no final, ou seja, o total de movimentos que o cavalo fez é igual a quantidade de movimentos do peão para chegar no final. O -1 é necessário, uma vez que o peão começa jogando, então no final o cavalo irá fazer 1 movimento a menos.
Um exemplo de implementação segue abaixo: