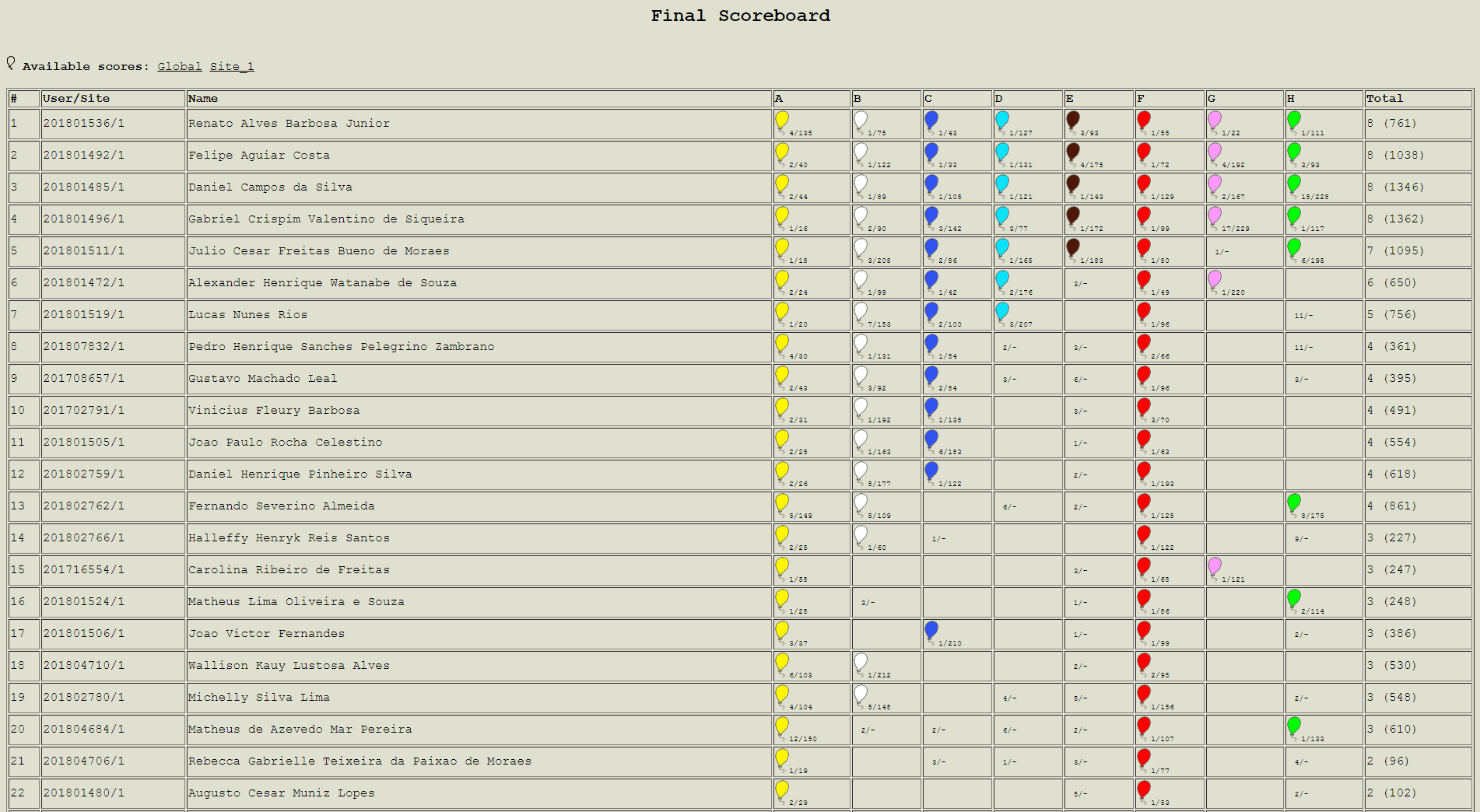
Aconteceu em 03 de Outubro de 2018 a 1ª Competição de Programação - 2018/2 do INF-UFG. O placar final da competição pode ser visto na imagem abaixo:
Parabéns à todos que participaram. O vencedor dessa competição, Renato Alves Barbosa Junior, ganhou um Power Bank 10000mA. Os dez primeiros participantes foram premiados com uma camiseta e brindes. Abaixo segue a lista dos ganhadores:
1ª Renato Alves Barbosa Junior
2ª Felipe Aguiar Costa
3ª Daniel Campos da Silva
4ª Gabriel Crispim Valentino de Siqueira
5ª Julio Cesar Freitas Bueno de Moraes
6ª Alexander Henrique Watanabe de Souza
7ª Lucas Nunes Rios
8ª Pedro Henrique Sanches Pelegrino Zambrano
9ª Gustavo Machado Leal
10ª Vinicius Fleury Barbosa
Para quem deseja tentar novamente, ou submeter usando outras ideias, os problemas estão disponíveis para submissão no HackerRank.
A prova foi composta por 8 problemas. Os níveis dos problemas e as respectivas técnicas que podem ser usadas para resolvê-los são apresentados na tabela abaixo:
| Problema | Dificuldade | Técnica relacionada |
|---|---|---|
| A - Bolo | Fácil | Ad hoc |
| B - Computadores | Médio | Guloso |
| C - Soma máxima | Médio | Guloso |
| D - Dados | Fácil | Matemática |
| E - Log bactérias | Médio | Matemática |
| F - Sinuca | Fácil | Implementação |
| G - Subcadeia interessante | Médio | String + Ad hoc |
| H - Melancias | Fácil | Ad hoc |
As explicações dos problemas seguem abaixo:
A - Bolo
Autor: Paulo Kataki
Enunciado: Bolo
Resolva este problema: Hackerrank
A solução desse problema é bastante simples. É sempre possível repartir um bolo de tamanho par maior do que 2 em dois pedaços de tamanho par maiores que 0. E é sempre impossível repartir um bolo de tamanho ímpar assim como um bolo de tamanho 2 seguindo as restrições do problema.
Um exemplo de implementação segue abaixo:
B - Computadores
Autor: Leandro Vianna
Enunciado: Computadores
Resolva este problema: Hackerrank
Existe uma escolha de lojas que é sempre mais vantajosa para Longo, escolher a loja de menor preço e comprar o máximo de computadores com o dinheiro do momento. Portanto, basta ordenar as lojas de forma crescente pelo preço dos computadores, e percorrer em sequência da loja de menor preço para a de maior preço, sempre tentando comprar a maior quantidade de computadores possível.
Para calcular quantos computadores é possível comprar com o dinheiro atual, basta dividir o dinheiro atual pelo preço do computador da loja que está sendo testada no momento. O piso deste valor é a quantidade de computadores que poderá ser comprada.
Assim, a cada iteração, basta retirar do dinheiro atual a quantidade de computadores comprados multiplicado pelo preço do computador nesta loja, ou seja, quanto foi gasto com computadores nesta loja. Deve ser mantida uma variável auxiliar inicializada com zero, e a cada iteração somar quantos computadores foram comprados, após as iterações esta variável conterá a resposta do problema, ou seja, a quantidade máxima de computadores que poderão ser comprados.
Um exemplo de implementação segue abaixo:
C - Soma Máxima
Autor: Rafael Castro
Enunciado: Soma
Resolva este problema: Hackerrank
O primeiro passo da solução será aplicar o máximo possível de operações sobre os números negativos (se eles existirem), começando do menor número negativo até o maior. Se após aplicado o primeiro passo ainda sobrarem algumas operações, então escolha o menor número Ai atual, e aplique as operações restantes sobre Ai, que pode ser feito aplicadas uma a uma ou apenas olhando a paridade desta quantidade restante. Assim, será garantido que as operações serão executadas de forma a gerar o maior valor possível.
O resultado será a soma dos números após executado os passos acima.
Um exemplo de implementação segue abaixo:
D - Dados
Autor: Welton Cardoso
Enunciado: Bolo
Resolva este problema: Hackerrank
Percebe-se que para um palíndromo de tamanho par (N % 2 == 0) basta olhar para os N⁄2 primeiros dados, pois o restante dos N⁄2 dados deverão refletir os N⁄2 primeiros para que a sequência de dados seja palindrômica. Por exemplo, suponha N = 6, as sequências palindrômicas terão o seguinte formato abccba, com 1 ⩽ a,b,c ⩽ 6. A probabilidade de se obter, em um próximo arremesso, uma sequência palindrômica será dado pelos eventos favoráveis sobre todas as possibilidades de eventos, ou seja, (6⌊N⁄2⌋)⁄6N.
Para o caso de uma sequência de tamanho ímpar (N % 2 != 0), o processo é parecido. Mas como o dado na posição N⁄2 + 1 poderá ter qualquer valor na sua face superior, então a probabilidade será (6⌊(N+1)⁄2⌋)⁄6N. Por exemplo, suponha N = 5, as sequências palindrômicas terão o seguinte formato abcba, com 1 ⩽ a,b,c ⩽ 6.
Percebe-se que ao considerámos o piso de N⁄2, então (6⌊N⁄2⌋)⁄6N = (6⌊(N+1)⁄2⌋)⁄6N quando N for par. Assim, podemos considerar o caso geral de N como (6⌊(N+1)⁄2⌋)⁄6N.
Um exemplo de implementação segue abaixo:
E - Log Bactérias
Autor: Misael Mateus
Enunciado: Log Bactérias
Resolva este problema: Hackerrank
Multiplique todos os elementos dos dois arrays e verifique qual gera o maior resultado. Como o valor dos elementos pode ser até 108, o produto dos elementos do mesmo array pode ultrapassar o valor suportado pelo inteiro de 32 bits. Para lidar com isso podemos usar o logaritmo.
Se a > b, onde a, b são positivos, então log(a) > log(b).
Usando as propriedades do logaritmo, temos que: log(a•b) = log(a)+log(b)
Então, basta somar o logaritmo de cada elemento do array e verificar qual dos dois arrays tem um resultado maior.
Um exemplo de implementação segue abaixo:
F - Sinuca
Autor: Leandro Vianna
Enunciado: Sinuca
Resolva este problema: Hackerrank
Como Thierson sempre escolhe jogar com as bolas ímpares, basta somar o valor de todos os números ímpares que estiverem na entrada. Tais números correspondem as bolas ímpares que estão em jogo no momento. Então, caso essa soma seja ímpar, imprima S, caso contrário, imprima N.
Um exemplo de implementação segue abaixo:
G - Subcadeia interessante
Autor: Paulo Kataki
Enunciado: Subcadeia interessante
Resolva este problema: Hackerrank
Para resolver esse problema basta ter algumas observações em relação à construção das cadeias interessantes. Por exemplo:
As cadeias com tamanho par, aa, aaab, aaaaab são cadeias interessantes. Podemos observar que todas têm pelo menos dois caracteres consecutivos iguais, no caso “aa”. Observa-se que a cadeia abab só poderá se tornar interessante caso se tenha aaab, bbab, abaa ou abbb, isso ocorre porque a quantidade de a’s e b’s correspondem a exatamente a metade do tamanho da cadeia analisada, logo se quisermos deixar ela interessante, o número de algum desses dois caracteres deve ultrapassar a metade e então teremos pelo menos 1 caractere repetido seguido de outro.
Para as cadeias de tamanho ímpar a análise não muda muito. Por exemplo: em aba, ababa, abababa todas já têm pelo menos um caractere no caso o “a” com a quantidade superior à metade. Logo a verificação consiste em olhar se têm dois caracteres iguais a uma distância 2.
A solução então é só varrer todos as posições da string s dada e verificar se há pelo menos uma posição i , tal que s[i] = s[i+1] , ou s[i] = s[i+2].
Um exemplo de implementação segue abaixo:
H - Melâncias
Autor: Humberto Longo
Enunciado: Melâncias
Resolva este problema: Hackerrank
Suponha que uma camada da pilha seja um triangulo com i melancias por lado. Isso significa que esse triangulo tem i + (i-1) + … + 1 melancias. Assim, basta começar da camada superior e, a cada iteração, aumentar uma camada e verificar se a quantidade total de triangulos excedeu o limite.
Um exemplo de implementação segue abaixo: