Aconteceu em 6 de Outubro de 2018 a 2ª Competição de Programação - 2018/2. A participação na competição foi restringida aos alunos que ingresseram no curso nos anos de 2017 e 2018. O placar final da competição, geral ou por semestre/ano, pode ser observado abaixo:

Para os(as) alunos(as) que desejam resolver os problemas, um replay da competição está disponível no HackerRank.

Parabéns à todos(as) que participaram. Como o placar da competição foi dividido de acordo com o ano de ingresso (2017 e 2018), o primeiro colocado de cada ano (vide abaixo) foi premiado com um MI BAND 2.

2017 Joao Batista de Oliveira Netto

2018 Felipe Aguiar Costa

Todos os participantes ganharam, além de brindes, uma camisa com o mascote (Monkey) do INF na Maratona de Programação.

A prova foi composta por 9 problemas. Os níveis dos problemas e as respectivas técnicas que podem ser usadas para resolvê-los são apresentados na tabela abaixo:

Problema	Dificuldade	Técnica relacionada
A - Desafio	Difícil	Ad hoc + XOR
B - Forró no cafundó	Fácil	Matemática
C - Obras	Médio	Guloso
D - Problemas do TAP	Médio	Ad hoc + Matriz
E - Brincando com múltiplos	Difícil	Princípio da inclusão-exclusão
F - Escadas	Médio	Programação Dinâmica
G - Campeonato de arco e flecha	Difícil	Busca binária
H - Terrenos	Médio	Matemática
I - Matriz espiral	Fácil	Implementação

As explicações dos problemas seguem abaixo:

A - Desafio

Autor: Paulo Kataki

Resolva este problema: Hackerrank

Esse problema parece ser bastante difícil, mas na verdade é bem simples. É necessário somente uma observação em relação a representação binária dos números. Por exemplo:

0 - 00
1 - 01
2 - 10
3 - 11
4 - 100
5 - 101
6 - 110
7 - 111
8 - 1000
9 - 1001
10 - 1010
11 - 1011

Podemos repartir esses números em blocos de tamanho 4:

Bloco 1
0 - 00
1 - 01
2 - 10
3 - 11

Bloco 2
4 - 100
5 - 101
6 - 110
7 - 111

Bloco 3
8 - 1000
9 - 1001
10 - 1010
11 - 1011

Dessa forma podemos ver que sempre há a repetição dos sufixos 00, 01, 10 e 11. O resto da representação é a mesma em todos os números pertencentes a esse bloco. Como a quantidade de 1’s e 0’s em cada posição é par, então o XOR de todos os números de um bloco é 0. Podemos então, dado um número N, encontrar sua posição no bloco correspondente e fazer o XOR desse valor com todos os números menores que N em tal bloco. A solução tem complexidade O(1).

Um exemplo de implementação segue abaixo:

B - Forró no cafundó

Autor: Paulo Kataki

Resolva este problema: Hackerrank

Dois números consecutivos são sempre primos entre si pois um número será sempre par e o outro sempre ímpar, logo não há um divisor comum entre eles exceto o 1. Como cada ingresso é único e cada dois números consecutivos não têm um divisor em comum exceto o 1, deve-se verificar apenas a paridade de n e se n > 0.

Um exemplo de implementação segue abaixo:

C - Obras

Autor: Paulo Kataki

Resolva este problema: Hackerrank

Este problema é uma variação do problema de escalonamento de tarefas. Podemos olhar as posições das extremidades de uma viga como um intervalo (x,y). Após isso, realiza-se um ordenação destes intervalos de acordo com o valor de x e depois deve-se utilizar um algoritmo guloso para agrupar os intervalos que têm uma intersecção e adicioná-los à resposta.

Um exemplo de implementação segue abaixo:

D - Problemas do TAP

Autor: Welton Cardoso

Resolva este problema: Hackerrank

O problema pede que dada uma matriz A, com dimensões N x M, onde pode-se escolher qualquer posição (i, j) de A, 1 < i < N e 1 < j < M, e eliminar todos os elementos da linha i e da coluna j. Ou seja, a matriz será dividida em quatro quadrantes. O enunciado segue com algumas definições. O maior valor em um quadrante é definido como interessante. A diferença entre o maior e o menor dos quatro valores interessantes é definido como atraente. Por fim, o valor fascinante da matriz é o maior valor atraente dentre todas as possíveis divisões da matriz em quadrantes.

Uma primeira tentativa de solução seria percorrer toda a matriz e simular as remoções da linha i e coluna j, bem como descobrir o maior valor de cada quadrante resultante da divisão da matriz A. Tal solução tem complexidade O(N · M · (N + M)). Ou seja, supondo que N = M, a complexiade seria O(N³) = O(1000³) = O(10⁹) o que não seria aceito no tempo. Percebe-se que uma solução O(N²) = O(10⁶) seria aceita tranquilamente. No entanto, o processo para descobrir o maior valor de um quadrante teria que ser em O(1). ♫ Para a nossa alegria ♫ é possível computar o maior valor de um quadrante em O(1) através de um pré-processamento.

Este pré-processamento deve ser feito para cada quadrante da matriz. Mas, neste primeiro momento, será explicado a ideia para o quadrante superior esquerdo. Já nos demais quadrantes o procedimento será análogo. Suponha um quadrante Q com 1 linha e 5 colunas. A ideia consiste em dada uma determinada posição Q_[1,j], com j ⩽ 5, tal posição deverá manter o maior valor entre as posições Q_[1,1] e Q_[1,j]. Assim, a primeira posição Q_[1,1] receberá o valor associado a mesma posição na matriz A. Já a próxima posição, Q_[1,2], deverá receber o maior valor entre tal posição posição associada à matriz A e a posição anterior, Q_[1,1]. Tal procedimento é ilustrado na figura abaixo. Assim, cada posição no quadrante Q terá o maior valor entre tal posição e as anteriores.

Tal procedimento resolve os quadrantes com uma única linha, mas e o caso dos quadrantes em que há varias linhas e uma única coluna? De forma análoga, cada linha deverá manter o maior valor entre essa linha e as linhas anteriores. O procedimento é idêntico ao aplicado ao quadrante com uma única linha, como ilustrado na figura abaixo.

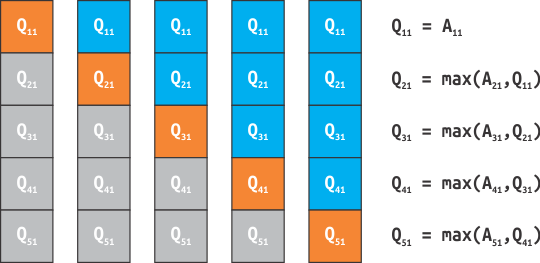
Agora é possível responder em O(1) qual é o maior valor de uma determinada posição de um quadrante supeior esquerdo de dimensões 1 x M ou N x 1. No entanto, ainda não é possível responder a mesma questão para um quadrante com dimensões N x M.

Suponha um quadrante superior esquerdo Q com dimensões 5 x 5. Suponha também que a primeira linha e a primeira coluna de tal quadrante tenha passado pelos procedimentos descritos anteriormente. Ou seja, para cada posição Q_[1,j] tenha o maior valor entre Q_[1,1] e Q_[1,j]. De forma análoga, a posição Q_[i,1] possua o maior valor entre Q_[1,1] e Q_[i,1]. A figura abaixo ilustra tal quadrante.

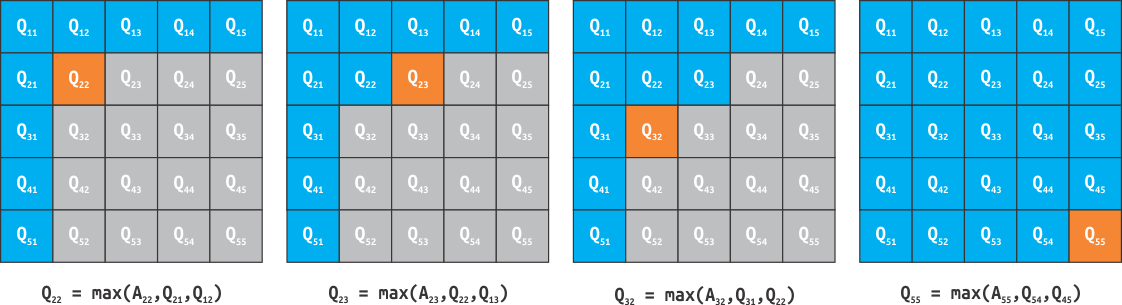
Note-se que a posição Q_[2,2], que representa o subquadrante {Q_[1,1],Q_[2,2]}, contém o maior valor dentro desse subquadrante ao fazer Q_[2,2] = max(A_[2,2],Q_[2,1],Q_[1,2]). Da mesma forma, a posição Q_[2,3], que representa o subquadrante {Q_[1,1],Q_[2,3]}, mantém o maior valor dentro de tal subquadrante ao fazer Q_[2,3] = max(A_[2,3],Q_[2,2],Q_[1,3]). Por fim, a posição Q_[3,2] retém o maior valor ao fazer Q_[3,2] = max(A_[3,2],Q_[3,1],Q_[2,2]). Ao seguir tal procedimento nas demais posições do quadrante percebe-se que a posição Q_[5,5] terá o maior valor do quadrante Q. Portanto, após tal procedimento, qualquer posição Q_[i,j] terá o maior valor dentre todas as posições do subquadrante {Q_[1,1],Q_[i,j]}.

Esse último procedimento resolve o problema de encontrar o maior valor dentro de um quadrante N x M. O pré-processamento consiste em realizar tal procedimento para os demais quadrantes: superior direito, inferior esquerdo e inferior direito. A figura abaixo ilustra o sentido em que se deve computar cada quadrante.

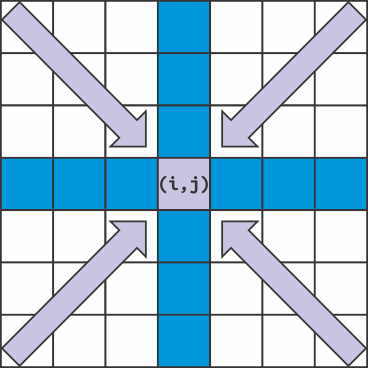
Assim, após o pré-processamento, para qualquer posição A_[i,j], o maior valor do quadrante:

• superior esquerdo estará na posição Q_[i-1,j-1];
• superior direito estará na posição Q_[i-1,j+1];
• infeiror esquerdo estará na posição Q_[i+1,j-1];
• inferior direito estará na posição Q_[i+1,j+1]
.

Como mostrado na figura abaixo:

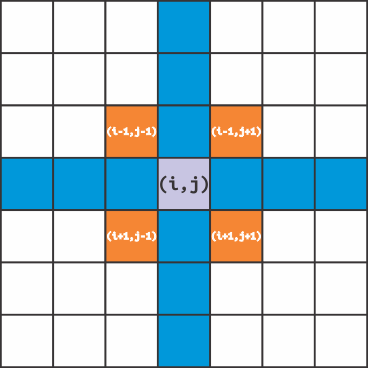
Com esses quatro valores interessantes (Q_[i-1,j-1], Q_[i-1,j+1], Q_[i+1,j-1] e Q_[i+1,j+1]) é possível computar o valor atraente_[i,j] da seguinte forma:

• atraente_[i,j] = max(Q_[i-1,j-1], Q_[i-1,j+1], Q_[i+1,j-1], Q_[i+1,j+1]) - min(Q_[i-1,j-1], Q_[i-1,j+1], Q_[i+1,j-1] e Q_[i+1,j+1]).

Ao percorrer cada posição A_[i,j], o valor fascinante poderá ser comptuado da seguinte forma:

• fascinante = max(fascinante, atraente_[i,j]).

Um exemplo de implementação segue abaixo:

E - Brincando com múltiplos

Autor: Paulo Kataki

Resolva este problema: Hackerrank

Esse problema é uma aplicação direta do princípio da inclusão e exclusão. Ou seja, podemos interpretar cada conjunto como sendo os múltiplos de cada um dos n valores dados como entrada. Também sabemos que a quantidade de múltiplos de um determinado número x num intervalo de 1 até m é ⌊ ^m⁄_x ⌋. Para gerar todas as combinações dos números podemos utilizar bitmasks.

Um exemplo de implementação segue abaixo:

F - Escadas

Autor: Paulo Kataki

Resolva este problema: Hackerrank

Esse problema pode ser resolvido com uma técnica chamada programação dinâmica. A relação de recorrência é a mesma que gera a sequência de Fibonacci porém calculado com o valor módulo 10⁹ + 7.

Um exemplo de implementação segue abaixo:

G - Campeonato de arco e flecha

Autor: Welton Cardoso

Resolva este problema: Hackerrank

O problema pede para que seja desenvolvido um programa que seja capaz de processar duas consultas:

• 1 a: O competidor alvejou um círculo com área a. Informe a pontuação obtida por ele.
• 2 a v: A organização alterou o valor do círculo com área a para o valor v.

Percebe-se que se fosse apenas a primeira consulta o problema seria mais simples. Uma vez que bastaria manter o acumulado do primiero círculo até o último círculo. Ou seja, cada círculo já teria a pontuação computada o que permitiria responder a consulta em O(1). No entanto, a segunda consulta modifica o valor associado a um determinado círculo, por conseguinte, torna-se necessário atualizar o acumulado dos círculos posteriores com área maior.

Essa atualizaçao apresenta complexidade, no pior caso, O(Q · N). Como o enunciado informa que a quantidade de consultas do tipo 2 a b será menor ou igual ao min{100, Q}, tem-se a complexidade O(100 · 100000) o que é suficiente para passar no tempo. Certo, consegue-se então atualizar toda vez os acumulados dos círculos, mas e a primeira consulta? Aqui, pode-se utilizar uma busca binária para descobrir a posição do círculo com área a. O porquê da necessidade da busca binária se dá pelo fato de não ser possível acessar um determinado círculo em um vetor diretamente indexado pela sua área. Por exemplo, suponha um vetor vet com 3 círculos (áreas 100, 150 e 1000000000). É possível indexar os dois primeiros círculos nas seguintes posiões do vetor: vet[100] e vet[150], já o terceiro não é possível, uma vez que não há memória disponível para tal alocação (vet[1000000000]).

Para exemplificar a solução observe o primeiro caso de teste do problema:

Será necessário armazenar as informações dos círculos e o acumulado das pontuações em vetores. Os vetores Área, Pontuação e Acumulado serão tais vetores nesta explicação. Note-se que o vetor Área mantém os valores da entrada de forma ordenada. Tal ordenação é necessária para que a busca binária possa ser realizada.

A primeira consulta, 1 2, deseja descobrir a pontuação após acertar o círculo com área 2. Assim, faz-se necessário realizar uma busca binária no vetor Área para descobrir em qual posição se encontra o círculo com área 2. Tal busca irá retornar a posição 1 do vetor Área (haja visto que a áera 2 está na posição 1). Desta forma, pode-se imprimir o valor associado à posição 1 do vetor Acumulado, que, no caso, será 1.

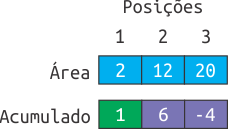
A segunda consulta é do mesmo formato que a primeira, logo, após uma busca binária, o círculo com área 20 será encontrado na posição 3 do vetor Área. Portanto, a respota estará na posição 3 do vetor Acumulado, que no caso é -4.

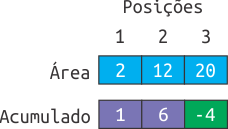
A terceira consulta é do segundo tipo. Assim, ao atualizar o valor da pontuação associado ao círculo com área 12 para 10 também será necessário atualizar o vetor Acumulado. Tal área se encontra na posição 2 do vetor Área, logo o vetor Acumulado na posição 2 deverá ser atualizado para Acumulado[2] = Acumulado[1] + 10. Do mesmo modo, na posição 3 para Acumulado[3] = Acumulado[2] + (-10).

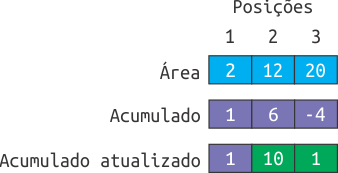
As demais consultas, 1 12 e 1 20, podem ser respondidas de forma análoga às primeiras consultas.

Um exemplo de implementação segue abaixo:

H - Terrenos

Autor: Leandro Vianna

Resolva este problema: Hackerrank

Basta verificar se N é um quadrado perfeito, ou seja, se existe um número x tal que x · x = N, e se x é um número primo. Existem várias abordagens. Uma delas é percorrer através de um loop os valores de 2 até √N com o intuito de encontrar um divisor de N, ou seja, um candidato para o x mencionado anteriormente. Verifique se x · x = N, caso contrário imprima “N”. Então verifique se x é um número primo, o que pode ser feito percorrendo de 2 até √x, se algum destes números dividir x, então imprima “N” já que x não é primo, pois x tem um divisor diferente de 1 e x. Caso não encontre um divisor para x, imprima “S”, já que √N e x é um número primo.

No pior caso esse código percorre √N números mais √x no loop interno. Se x = O(√N), a complexidade dessa solução será O(√N + √N) = O(√N). Como N ⪁ 10¹² essa solução passa no tempo limite. Um exemplo de implementação segue abaixo:

I - Matriz espiral

Autor: Misael Mateus

Resolva este problema: Hackerrank

Este problema pode ser resolvido com uma matriz auxiliar que informa quais as posições já foram percorridas. Assim, quando encontrar uma posição já percorrida ou que leve para fora da matriz poderá mudar de direção. O sentido do percurso deverá respeitar o setindo da espiral, ou seja, direita → para baixo → esquerda → para cima.

Um exemplo de implementação segue abaixo: