TAP-2019/1 - Treino 1

Aconteceu em 15 de Março de 2019 o primeiro treino da disciplina TAP - Tópicos Avançados de Programação. O placar atual do treino pode ser visto na imagem abaixo.

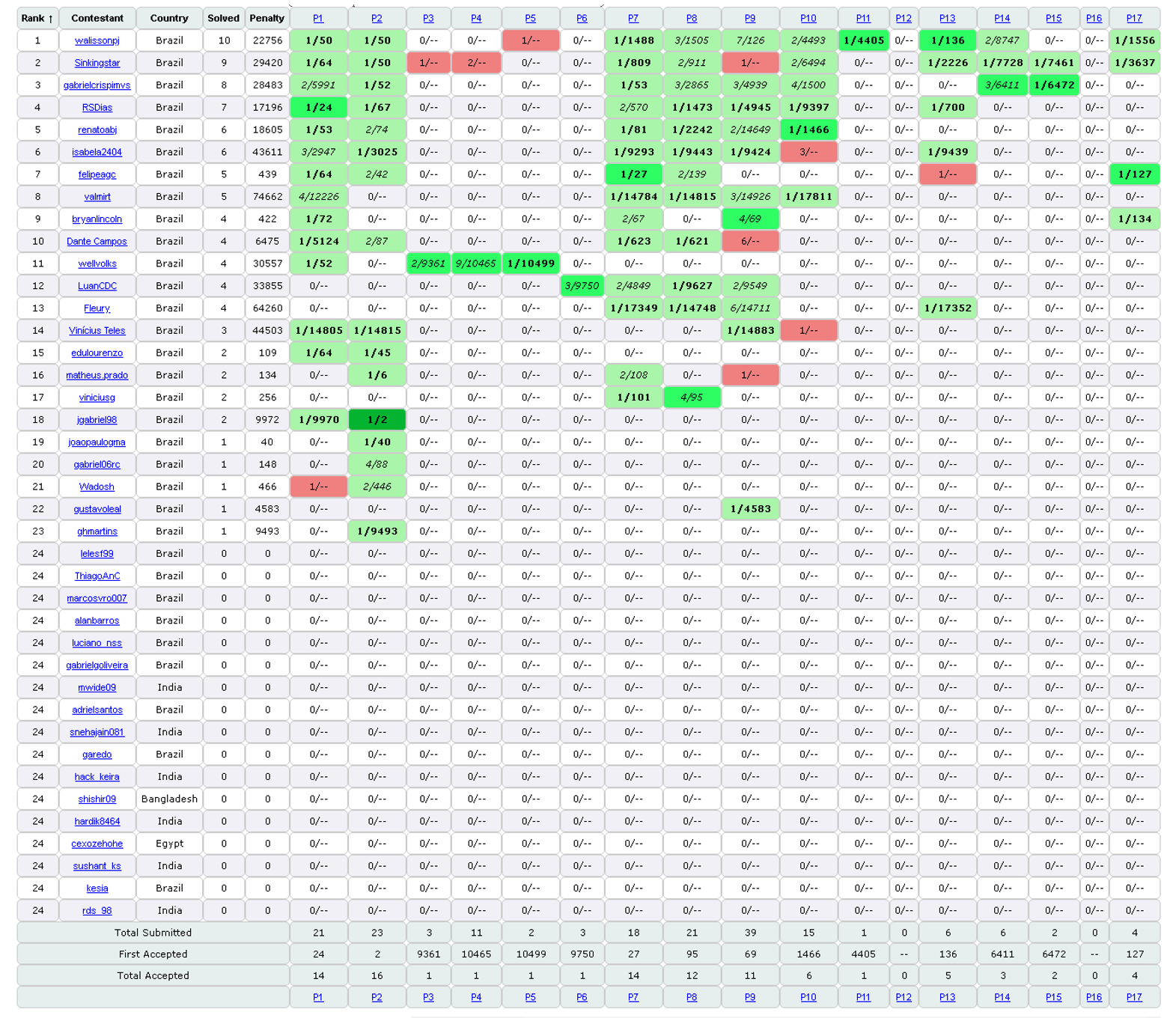
A lista de exercícios foi composta por 17 problemas. Os níveis dos problemas e as respectivas técnicas que podem ser usadas para resolve-los são apresentados na tabela abaixo.

Problema	Dificuldade	Técnica relacionada
P1 - Macaco rural	1	Ad hoc
P2 - Aeroporto	1	Ad hoc
P3 - Penta!	3	STL-Set
P4 - Monitorando a Amazônia	6	Ad hoc + Matriz
P5 - Jogo da vida	4	Simulação + STL-Map
P6 - Linear Cellular Automata	1	Implementação
P7 - The Decoder	1	=)
P8 - Kindergarten Counting Game	1	Implementação
P9 - Fibonacci Freeze	2	Big Number
P10 - Quirksome Squares	3	Ad hoc
P11 - Divisors	5	Matemática
P12 - Interpreting Control Sequences	3	Implementação
P13 - Big Mod	4	Fast Modular Exponentiation
P14 - Perfect Cubes	3	Ad hoc + Map
P15 - The Seasonal War	3	DFS
P16 - Interpreter	4	Implementação
P17 - Ananagrams	4	STL-Map + Ordenação

P1 - Macaco rural

Resolva este problema: SPOJ

O problema pede para agrupar os 2n produtos em n pares de forma tal que o custo do par mais caro seja minimizado. O custo de um par é a soma dos custos dos produtos que o compõem. Percebe-se que para minimizar o custo de um par, o produto mais caro deverá ser combinado(somado) com o produto mais barato, já que qualquer outra combinação irá resultar em uma soma maior ou igual. Em seguida, a próxima combinação mínima constituirá da soma do penúltimo produto mais caro com o segundo produto mais barato, depois o antepenúltimo com o terceiro e assim por diante até que não haja mais produtos para serem combinados. Tais combinações irão resultar nas menores somas possíveis. Desta forma, após computa-las, basta descobrir quais delas apresenta a maior soma.

Um exemplo de implementação segue abaixo:

P2 - Aeroporto

Resolva este problema: SPOJ

Como programador recém contratado pela ATAI você foi encarregado de escrever um programa para determinar, a partir de uma listagem de aeroportos e voos, qual aeroporto possui maior probabilidade de congestionamento no futuro. Como medida da probabilidade de congestionamento será utilizado o número total de voos que chegam ou que partem de cada aeroporto. Assim, basta computar esses totais e descobrir quais desses valores é o maior. Em seguida, imprimir todos os aeroportos que tenham essa maior quantidade total de voos.

Um exemplo de implementação segue abaixo:

P4 - Monitorando a Amazônia

Resolva este problema: SPOJ

Um exemplo de implementação segue abaixo:

P3 - Penta!

Resolva este problema: SPOJ

Com o dinheiro recebido como prêmio pela conquista da Copa do Mundo os jogadores decidiram contratar os seus serviços. Você deve escrever um programa que determine o número mínimo de trocas de jogadores no palanque, conhecendo a lista formulada por Felipão e sabendo que os jogadores desejam ficar no palanque a maior quantidade tempo possível.

Antes de explicar uma solução para esse problema, faz-se necessário apresentar as três situações referente ao palanque.

• 1º situação: o palanque tem vaga e o próximo da lista não está no palanque. Nesse caso, basta o jogador subir no palanque.
• 2º situação: o palanque tem vaga e o próximo da lista já está no palanque. Nesse caso, não haverá movimentação de jogadores.
• 3º situação: o palanque está cheio e o próximo da lista não está no palanque. Nesse caso, um dos jogadores que está no palanque deverá descer e próximo da lista deverá subir, por conseguinte será contabilizado uma troca.
• 4º situação: o palanque está cheio e o próximo da lista já está no palanque. Nesse caso, não haverá troca de jogadores.

Dentre as quatro situações, a única problemática é a terceira. Qual jogador deverá descer para que o próximo da lista suba no palanque? Escolher um jogador que está a mais tempo no palanque parece ser o mais justo, no entanto, uma vez que tal jogador pode aparecer logo em seguida na lista, tal escolha irá resultar em mais uma troca futuramente. Uma outra estratégia é escolher o jogador que terá que estar no palanque novamente o mais tardar possível dentre os demais jogadores no palanque. Assim, os jogadores que em breve terão que estar no palanque novamente tem uma maior prioridade dentre os outros para ficar no palanque. Desta forma, a quantidade de trocas de jogadores será reduzida.

O controle de quem está ou não no palanque pode ser feito por um set de pair < int , int >, onde a primeira posiçao do pair representa o próximo momento que o jogador, cujo identificador está na segunda posição do pair, deverá estar no palanque novamente. Note-se, que na terceira situação o jogador que deverá descer estará na última posição do set, uma vez que tal jogador terá o próximo momento no palanque o mais distante possível se comparado aos demais jogadores no palanque.

Um exemplo de implementação segue abaixo:

P5 - Jogo da vida

Resolva este problema: SPOJ

Um exemplo de implementação segue abaixo:

P6 - Linear Cellular Automata

Resolva este problema: UVA

Um exemplo de implementação segue abaixo:

P7 - The Decoder

Resolva este problema: UVA

Um exemplo de implementação segue abaixo:

P8 - Kindergarten Counting Game

Resolva este problema: UVA

Um exemplo de implementação segue abaixo:

P9 - Fibonacci Freeze

Resolva este problema: UVA

Um exemplo de implementação segue abaixo:

P10 - Quirksome Squares

Resolva este problema: UVA

Um exemplo de implementação segue abaixo:

P11 - Divisors

Resolva este problema: SPOJ

Um exemplo de implementação segue abaixo:

P12 - Interpreting Control Sequences

Resolva este problema: UVA

Um exemplo de implementação segue abaixo:

P13 - Big Mod

Resolva este problema: UVA

Um exemplo de implementação segue abaixo:

P14 - Perfect Cubes

Resolva este problema: UVA

Um exemplo de implementação segue abaixo:

P15 - The Seasonal

Resolva este problema: UVA

Um exemplo de implementação segue abaixo:

P16 - Interpreter

Resolva este problema: UVA

Um exemplo de implementação segue abaixo:

P17 - Ananagrams

Resolva este problema: UVA

Um exemplo de implementação segue abaixo: